WisFaq!

Stabiele en instabiele dekpunten zoeken

Hallo

Van f(x)=x²-(1/4), zou ik graag de dekpunten vinden...

Ik loste de vergelijking (x²-(1/4)=x) op en vond: (1±Ö2)/2.

Maar als ik met de rekenmachine iteraties uitvoer met omliggende punten kom ik steeds -0,5 en 0,5 uit (Na herhaaldelijk itereren...)

Wat is nu het stabiel en wat het instabiel dekpunt?
Of zijn -0,5 en 0,5 de twee stabiele dekpunten?

Miguel
20-1-2005

Antwoord

Hoe je op -0,5 en 0,5 uit kunt komen is me een raadsel.
Kijk maar in onderstaande webgrafiek:



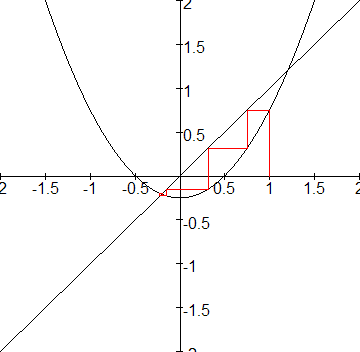
Het instabiele dekpunt is(1+Ö2)/2.
Het stabiele dekpunt is (1-Ö2)/2.
Dit kun je ook berekenen door in beide dekpunten f '(x) uit te rekenen en na te gaan of |f '(x)|1.
|f '((1+Ö2)/2)|=1+Ö21
|f '((1-Ö2)/2)|=|1-Ö2|1.

hk
20-1-2005