Van een lineaire afbeeldingT:
 3®
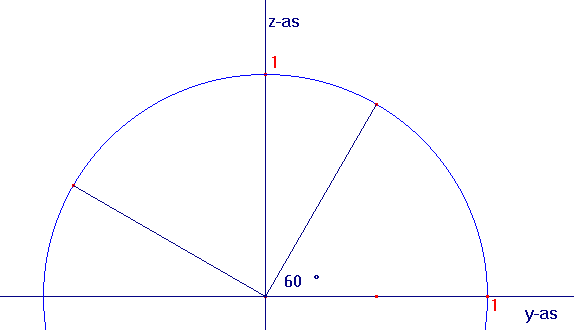
3® 3 wordt het beeld van een vector a als volgt verkregen: Eerst wordt a gedraaid over een hoek van 60° om de x-as (tegen de klok), vervolgens wordt de vector met een factor 4 vermenigvuldigd, en tenslotte wordt er gespiegeld in het vlak x=0 (het yz-vlak dus).
3 wordt het beeld van een vector a als volgt verkregen: Eerst wordt a gedraaid over een hoek van 60° om de x-as (tegen de klok), vervolgens wordt de vector met een factor 4 vermenigvuldigd, en tenslotte wordt er gespiegeld in het vlak x=0 (het yz-vlak dus). Vraag: Bepaal de matrix A van T.
Ik weet wel hoe ik dit moet aanpakken, maar ik weet niet hoe ik die 3 deelmatrices moet maken. Kan iemand mij stap voor stap (grafisch) uitleggen hoe ik die deelmatrices maak?
Bvd!
CT
3-1-2005