WisFaq!

Is de sinusfunctie even of oneven?

Is de sin-functie een even of oneven functie ?
y=sin x heeft volgens mij een symmetriepunt in de oorsprong
en daarom is het een oneven functie ? sin(-x) = - sin x
maar de cos functie is een even functie
maar de cos-functie is toch een verschuiving van de sin-functie ?
dus waarom is de sin-functie ook niet even ? :/
dank bij voorbaat

Dave
5-12-2004

Antwoord

Even jezelf voorstellen wat er gebeurt.
Laten we maar eens wat andere functies nemen.
Neem b.v. f(x)=x². Deze functie is lijnsymmetrisch in de lijn x=0(de y-as). Deze functie is even.
Schuif je deze functie 1 naar rechts op. Wat wordt dan de symmetrie?: lijnsymmetrisch in de lijn x=1. Het functievoorschrift is y=(x-1)²=x²-2x+1. Dus als je de even functie y=x² horizontaal verschuift hoeft het resultaat dus helemaal niet meer een even functie te zijn. Net zo goed; als je een oneven functie horizontaal verschuift dan hoeft het resultaat helemaal niet meer een oneven functie te zijn.

Nu even de functies sin en cos.

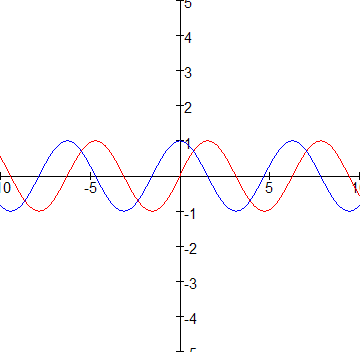
De grafiek van sin (de rode grafiek) is puntsymmetrisch in de oorsprong, sin(-x)=-sin(x).
Maar: de grafiek van sin heeft nog meer symmetrieassen en symmetriepunten: b.v. de grafiek van sin is ook lijnsymmetrisch in de lijn x=¹/₂p.
Schuif je de grafiek van sin dus ¹/₂p naar links op dan is de verschoven grafiek (de blauwe grafiek) lijnsymmetrich in de lijn x=0. Laat die verschoven grafiek nu juist de grafiek van cos zijn!
Kortom de functie cos is even: cos(-x)=cos(x)

hk
5-12-2004