WisFaq!

Optimalisatie van een simpele functie

Gegeven:

f(x) = x · sin(10p · x) + 1.0
f'(x) = sin(10p · x) + 10px · cos(10p · x) = 0

Dit is gelijk aan:

tan(10p · x) = -10px

Er zijn voor deze vergelijking oneindig veel oplossingen.
Tot hier is alles duidelijk.

x_i = (2i-1) / 20 + e_i, voor i = 1, 2,...
x₀ = 0
x_i = (2i+1) / 20 - e_i, voor i = -1, -2,....

e_i stelt een reeel nummer voor dat 0 nadert voor
i = 1,2,... en i = -1,-2,....

Hoe zijn ze aan bovenstaande gekomen?
Ik had dit in mijn hoofd (geleerd op de middelbare school):

tan(10p · x) = -10px
tan(10p · x) = tan(tan^-1(-10px))
10p · x = tan^-1(-10px)) + k·p
x = ^{tan-1(-10px))}/_10p + ^k·p/_10p
x = ^{tan-1(-10px))}/_10p + ^k/₁₀

Robert
19-11-2004

Antwoord

dag Robert,

Op de middelbare school heb je waarschijnlijk alleen vergelijkingen gekregen van de vorm
tan(x) = a
en die los je inderdaad op op de manier die je schetst.
Maar omdat de onbekende x hier zowel in het linkerlid onder de tan-functie, als in het rechterlid voorkomt, werkt die methode niet. Je kunt de x niet vrijmaken.
De gegeven vergelijking kan wel numeriek aangepakt worden.
Het komt in feite neer op de vergelijking
tan(t) = -t

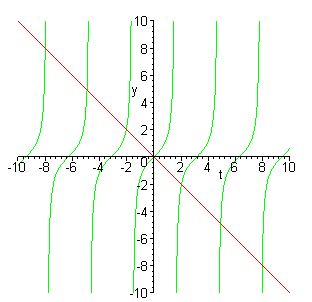
De grafieken van tan(t) en -t in een figuur laten zien, waar de snijpunten zich bevinden: hoe groter t, hoe dichter het snijpunt bij de asymptoot ligt.
Vandaar die e_i die naar 0 naderen.
groet,

Anneke
19-11-2004