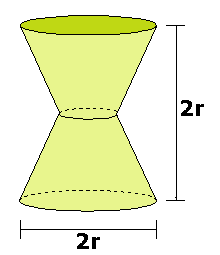
 Zie de afbeelding hiernaast.
Zie de afbeelding hiernaast.De inhoud van één zo'n afgeknotte piramide is:
1/3·$\pi$r2·2r-1/3·$\pi$(1/2r)2·r=...
..en daar heb je er dan twee van!
Zou moeten kunnen zou ik denken...
WvR
18-10-2004
Halo, ik heb weer een probleem; twee congruente kegels met een hoogte gelijk aan 2 keer de straal R van hun grondvlak hebben een gemeenschappelijke as en zijn zodanig geplaatst dat elk van hen zijn top heeft in het grondvlak van de andere. bereken het volume van de 2 kegels.
het volume van de kegel : 1/3·$\pi$·r2·h
ik vervang h door r en krijg
1/3·$\pi$·r3 = V
nu heb ik 2 van die kegels dus :1/3·$\pi$·r3 + 1/3·$\pi$·r3 = 2/3·$\pi$·r3 = V maar dat klopt niet het moet 7/6·$\pi$·r3 = V
kan iemand me misschien met dit probleem helpen?
bedanktwinny
18-10-2004
Zie de afbeelding hiernaast.
De inhoud van één zo'n afgeknotte piramide is:
1/3·$\pi$r2·2r-1/3·$\pi$(1/2r)2·r=...
..en daar heb je er dan twee van!
Zou moeten kunnen zou ik denken...
WvR
18-10-2004
#28698 - Oppervlakte en inhoud - 2de graad ASO