WisFaq!

Re: De diagonalen in het vierkant in de parallellogram?

Sorry, ik heb het nog eens nader gevraagd. Ik bedoelde eigelijk geen vierkant maar een gewoon rechthoek. En dat rechthoek wordt dan gevormd door de bisectrices van het parallellogram. Het snijpunt van de diagonalen van dat rechthoekje is hetzelfde snijpunt als hetsnijpunt van de diagonalen van het parallellogram.

Bedankt, ik hoop dat dit wel de goede formulering is.

B. de Graaf
28-9-2004

Antwoord

Goeidag

Sorry voor het lange wachten. Dus een rechthoek in een parallellogram:



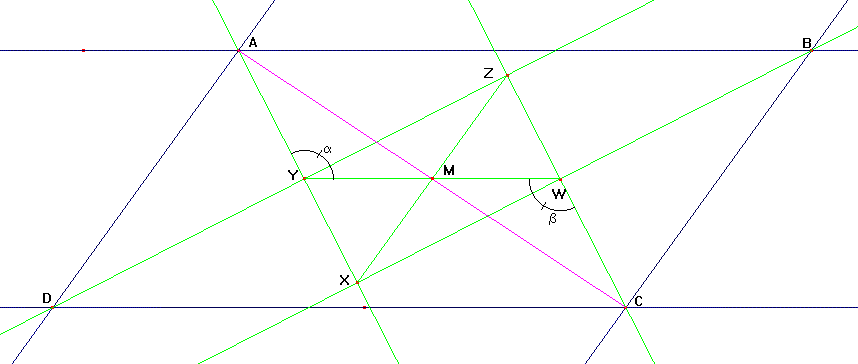
Ik veronderstel dat je mag aannemen dat WXYZ een rechthoek is, indien nodig kan je dit zelf ook bewijzen. Het punt M is het het middelpunt van de rechthoek. Nu moeten we bewijzen dat M ook het middelpunt van het parallellogram is. Als we kunnen aantonen dat D AMY congruent is met D CMW, dan volgt daaruit wat je moet bewijzen (denk daar eens over na). Die congruentie bewijzen kan via ZHZ.

|YM|=|WM| (diagonalen van een rechthoek snijden elkaar middendoor)
a=b (volgt uit evenwijdigheid van de lijnen YX & ZW)
|AY|=|CW| (dit volgt uit de congruentie van DAYD en DCWB, probeer dit zelf eens te bewijzen)

Groetjes
Igor

Igor
2-10-2004