WisFaq!

Limiet uit de film `Mean Girls`

Hoi vrienden ;
lim van x-- 0 van (ln(1-x)-sinx)/(1-cos²x)

deze limiet komt uit de film " Mean Girls" , waarin een meisje uitlegt dat de film niet bestaat . Ok , vreemd gegeven , maar nu moeten wij bewijzen dat de limiet wel bestaat voor school :s En niemand weet precies goed hoe te beginnen

Dirk
15-9-2004

Antwoord

Hoi

Lijkt me wel een toffe vraag van jullie leraar/lerares. We tekenen alvast de grafiek van de genoemde functie:

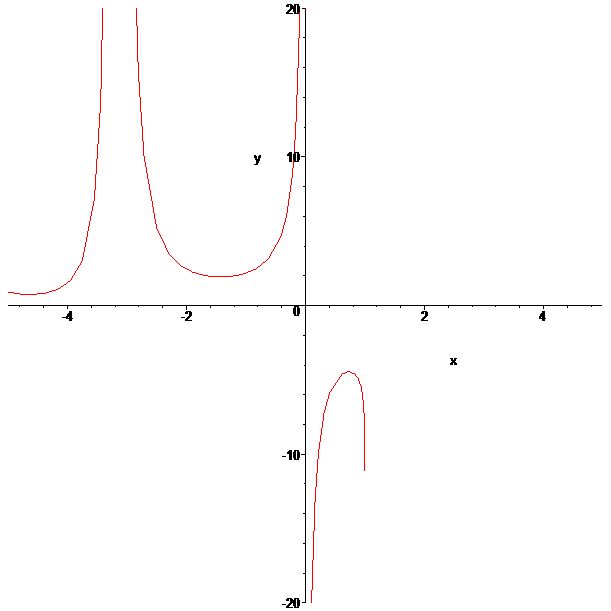Wat gebeurt er in nul? Links van nul wordt de de functiewaarde heel groot en rechts van nul wordt de functiewaarde heel klein. Met andere woorden, uit de grafiek blijkt dat de linkerlimiet in 0 gelijk is aan + ¥. De rechterlimiet in 0 daarentegen is gelijk aan - ¥. Omdat de linkerlimiet niet gelijk is aan de rechterlimiet, zegt men dat de limiet niet bestaat!!!!!!!! Misschien heeft dat meisje uit die film dan toch gelijk? Wat en slimme meid zeg!

Ik geef toe, door die grafiek te bekijken hebben we een beetje vals gespeeld, want misschien hebben jullie geen grafische rekenmachine. Daarom zal ik jullie op weg zetten bij de manuele berekening van de limiet!

Als jullie 0 invullen in de functie, bekomen jullie de onbepaalde vorm ⁰/₀. We kunnen dus de regel van de l'Hopital gebruiken. Indien je daar nog nooit van gehoord hebt, neem dan hier een kijkje. We vervangen eerst 1-cos²(x) in de noemer door sin²(x). Na toepassing van de regel van de l'Hopital wordt de limiet

=limit(x ® 0) ^{-1/_(1-x)-cos(x)}/_{2*sin(x)*cos(x)} omdat 2*sin(x)*cos(x)= sin(2*x), geldt:

=limit(x ® 0) ^{-1/_(1-x)-cos(x)}/_sin(2*x) We proberen nu opnieuw 0 in te vullen in de nieuwe functie. We bekomen dan ^-2/₀.

Vanaf nu zou je moeten weten hoe verder te doen. Jullie zullen dit wel gezien hebben. Ik geef je een tip: maak het tekenschema van de noemer (=sin(2*x)).

Als het je niet bekend overkomt, heeft jouw juf of leraar deze oefening misschien als voorbereiding meegegeven op de volgende wiskundeles. In dat geval, denk er eens over na!

Veel succes

Igor
15-9-2004