In werkelijkheid worden IQ scores beschouwd als normaal verdeeld met m=100 en s=15.
Willekeurige IQ scores kun je dus beschouwen als afkomstig uit deze verdeling. In jouw geval hebben de gemeten IQ scores een gemiddelde 105,63 en een steekproefstandaarddeviatie s=17,59. Iets hoger dus dan in de theoretische verdeling.
Nu wil je weten of de verschillen in IQ scores bij tweelingen kleiner zijn dan de verschillen in IQ scores van twee willekeurige personen. Ik neem aan dat de scores van die twee willekeurige personen afkomstig zijn uit een normale verdeling met m=100 en s=15.
Als verschilvariabele (bij IQ van twee personen) definieer je Vi=Maxi-Mini. Hier staat niets anders als: bij elk tweetal neem je het grootste - kleinste IQ.
De vraag is nu wat de verdeling van Vi zal zijn.
Zoiets dergelijks is gelukkig al eens (1951) uitgezocht: wanneer je twee waarnemingen pakt uit een standaardnormale verdeling zullen de verwachtingswaarde en standaarddeviatie van de variabele Max-Min respectievelijk 1,12838 en 0,72676 zijn. Neem verder maar even aan dat die verschilvariabele weer normaal verdeeld is**.
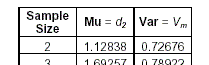
Deze waarden komen uit het artikel bij de onderstaande link. Probeer het einde van pagina 2 en pagina 3 te doorgronden.
Dat betekent dat bij twee trekkingen uit een standaard normale verdeling de variabele Max-Min een gemiddelde waarde heeft van 1,12838 en een standaarddeviatie van 0,72676.
Bij twee trekkingen uit een normale verdeling met m=100 en s=15 is de spreiding 15 keer zo groot en is de verwachtingswaarde bij Max-Min = 15·1,12838=16,9 en de standaarddeviatie is 15·0,72676=10,9.
Dit kun je zien als de (normale) verdeling die je krijgt als je het verschil (Max-Min) neemt van de IQ scores van twee willekeurige personen.
Je wil nu toetsen of bij tweelingen deze verschillen kleiner zijn. Dus toets je:
H0:mV=16,9
H1:mV
 16,9
16,9Dit is gewoon een toets voor een gemiddelde. Als toetsingsgrootheid neem je het gemiddelde van de 15 verschilwaarden Vi (0,8,11,7,1,20,4,2,24,3,8,7,11,4,1). Dit gemiddelde is 7,4. Een stuk lager dan die 16,9. Maar is dat ook significant?
De grens van het kritiek gebied bij bovenstaande toets is 16,9-z·s/Ön = 16,9-1,65·10,9/Ö15 = 12,3.
Dus de toetsingsgrootheid 7,4 is inderdaad significant lager.
Wat weet je nu: Het verschil in IQ's van (eeneiige) tweelingen is significant lager dan het verschil in IQ van twee willekeurige personen. Wat verder doordenkend mag je ook wel concluderen dat dit verschil gemiddeld minstens 4,9 IQ punten bedraagt.
Je weet dan echter alleen dat het verschil bij tweelingen significant kleiner is dan het verschil bij twee willekeurige personen. Maar of dat ligt aan de eeneiige tweelingen ?? Misschien ligt het wel aan de opvoeding of het gezin. Om dat te weten zou je bijvoorbeeld eeneiige tweelingen moeten vergelijken met normale broers of zusjes.
NB. Ik heb voor de standaarddeviatie 15 genomen. Dat is in ieder geval de veilige weg. Je zou er over kunnen discussieren of dat niet wellicht 17,59 had moeten zijn. Dan wordt het er overigens alleen maar beter op.
NB. Die 100 of 105,63 doen in het verhaal uiteindelijk niet terzake omdat je alleen naar verschillen kijkt.
NB. Onderstaand artikel (pag 4) geeft aan dat die normale verdeling bij ** niet helemaal correct is. Je zou moeten kijken naar een chi-kwadraat verdeling. Ik schat zo in dat in jouw geval dat niet zoveel uitmaakt.
Wel....... ik hoop dat het nog een beetje te volgen is...... en dat ik alles goed berekend heb. Nog even goed narekenen dus en nooit iets opschrijven dat je zelf niet snapt. Laat nog maar eens weten hoe dit bij je docenten ingeslagen is (als een .........)
Met vriendelijke groet
JaDeX
Zie Verdeling Max-Min bij stand.norm. verdeling [http://www.aiag.org/forms/StatExpose_d2.pdf]
jadex
11-9-2004