WisFaq!

Cosinusregel

In de wiskunde staat er bij het gebruik van de cosinusregel een minteken nl. c² = a² + b² - 2ab cosα
In de fysica zijn a en b zijn de groottes van de gegeven vectoren, c is de grootte van de resulterende vector die we zoeken en α is de hoek tussen beide vectoren. Als we in de fysica deze regel gebruiken om algebraïsch de grootte van de resultante c van twee vectoren te zoeken, staat er een plusteken!c²= a²+b²+2ab cosα
Hoe komt dit????

Charlotte Van Der Eecken
4-9-2004

Antwoord

Kijk eens naar dit plaatje:



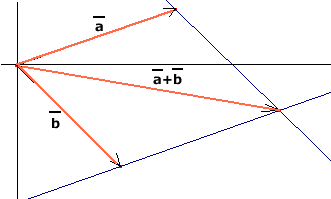
Met de cosinusregel zou je niet de lengte van a+b uitrekenen. Dat wil je wel...
Dus verschuif je de vector a (of b), dan krijg je een driehoek waarin je wel de lengte van a+b kan berekenen met de cosinusregel...
...en omdat de hoek dan 180°-a is zou je cos(180°-a) moeten nemen...
of je neemt -cos(a)...
...en wat denk je...
...krijg je (met de cosinusregel) toch:

c²=a²+b²+2abcosa

Hopelijk helpt dat...

WvR
4-9-2004