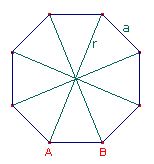
Bedenk dat je in het middelpunt van de omgeschreven cirkel steeds een hoek van 45° hebt zitten! Als je nu één van de acht driehoeken apart bekijkt, dan heb je een gelijkbenige driehoek ABC met benen AC en BC van 2 meter en met een tophoek C van 45°.Nu kun je óf de hoogtelijn vanuit C trekken, óf een hoogtelijn vanuit A of B.
In het eerste geval kun je verder omdat je weet dat $\angle$C gehalveerd wordt (gebruik goniometrie), en in het tweede geval ontstaat er een 'geodriehoek' (dus met twee hoeken van 45°), zodat je de hoogtelijn exact kunt berekenen.
Gebruik bijv. sin45° = ½√2.
Heb je eenmaal de oppervlakte van één driehoek te pakken, dan hoef je alleen nog maar met 8 te vermenigvuldigen.
Zie oppervlakte regelmatige n-hoek [http://www.wisfaq.nl/showrecord3.asp?id=1362]
MBL
14-4-2002