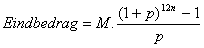WisFaq!

Gecombineerde annuďteiten

Iemand wil per 31 december 2009 de middelen beschikbaar hebben voor aanschaf van zomerhuisje. Sinds 1990 heeft hi jdaarvoor jaarlijks aan begin van ieder jaar € 200,- op spaarrekening met 7,2% rente gestort. Op 1 januari 2003 constateert hij dat de prijs v/h zomerhuisje is prijs is gestegen. Hij moet nu rekening houden met een prijs van € 125.000,- in het jaar 2010. Bovendien daalt de rente met ingang van 1 januari 2003 zo dat hij vanaf nu tot 2010 voor totale spaarbedrag slechts 6% interest p/j zal ontvangen.

A. bereken het bedrag dat hij dacht bij storting van € 2000,- per jaar en rente van 7% te moeten betalen voor het zomerhuisje

B. bereken het bedrag dat met ingang van 1 januari 2003 op de spaarrekening worden gestort om de aankoop plannen alsnog te kunnen uitvoeren

Ik kom hier echt niet uit [:'(]

Gérald
11-8-2004

Antwoord

Beste Gérald,

laat ons eens kijken:

A. Hier geraak je al ver mee met de annuďteitenformules:



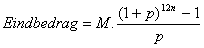
Ik heb snel die op maandbasis genomen, maar dat maak niet veel verschil uit (voor M jaarbedrag nemen en voor 12n het aantal jaar). Dan krijg je:
Eindbedrag = 2000 * ((1,072)²¹-1) / 0,072)
Eindbedrag = 91.837,87
Opmerking: het zijn 21 termijnen, want in jaar 2009 stort je in het begin, maar brengt nog gedurende heel 2009 intrest op.

B. Hiervoor heb je dezelfde formule nodig, alleen moet je die in 2 splitsen omdat je voor en na 1 januari 2003 andere gegevens hebt. Op dat moment zijn er al 13 stortingen gebeurd (tem 2002).

Het deel vanaf 2003 kunnen we als volgt voorstellen (met 6% intrest)
Eindbedrag door stortingen vanaf 2003 = bedrag * ((1,06)⁸-1) / 0,06)
= bedrag * 9,897467909

Voor het deel voor 2003 hebben we alle gegevens:
Bedrag op 1 januari 2003 = 2000 * ((1,072)¹³-1) / 0,072)
= 40.807,31

Het bedrag op 1 januari 2003 brengt natuurlijk nog 6% op tem 31 december 2009. Hiervoor kunnen we de formule voor enkelvoudige intrest gebruiken:
40.807,31 * [(1,06)⁸-1] = 24.233,34

Nu moeten we de 3 delen samenvoegen voor de eindwaarde die we kennen:
125.000 = bedrag * 9,897467909 + 40.807,31 + 24.233,34
Bedrag te storten vanaf 2003 = 6.058,05

Je kan al die delen natuurlijk ook meteen als 1 formule zetten: eindbedrag = ... + ... + ..., maar dat is natuurlijk minder overzichtelijk en zo maak je sneller fouten.

Groetjes,

Zie Voorbeeld met geld afhalen [http://www.wisfaq.nl/showrecord3.asp?id=12034]

tg
13-8-2004