WisFaq!

Coordinaten van een 3d vlakken stelsel

Hoi,

Een vriend van mij heeft een 3D figuur (kunstwerk) gemaakt van 18 vijfhoeken die allemaal netjes met hun zijdes tegen elkaar liggen en vraagt zich nu af wat de coordinaten zijn van alle hoekpunten, dit opdat het figuur echt gemaakt kan worden. De vijkhoeken zijn allemaal hetzelfde en uiteraard onregelmatig :-), de hoeken zijn 60,90,60,90,60 en alle zijdes zijn 1 behalve de laatste die is abs(1 - sqrt(3)). het geheel lijkt een beetje op een aperots.

De coordinaten van het eerste vijfhoekje zijn geen probleem, maar hoe reken ik daarna uit met welke verdraaiing de volgende vijfhoek hier aan vast zit?, Die verdraaiing wordt dus bepaald door het samenvoegen van drie vijfhoeken.

Veel dank,

Bas

Bas
8-8-2004

Antwoord

dag Bas,

Die hoeken van 60° moeten natuurlijk (stompe) hoeken van 120° zijn.
De 'korte' zijden van zo'n vijfhoek liggen altijd tegen een andere korte zijde aan.
Leg eerst vijfhoek nummer 1 op de grond. Leg vijfhoek nummer 2 met de korte zijde aan de korte zijde hieraan vast.

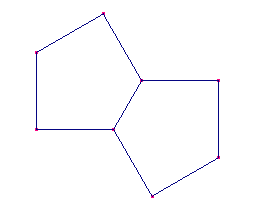
Nu vijfhoek nummer drie. Bekijk de hoek tussen de eerste twee vijfhoeken.
Zou hier nu een hoek van 120° tussen moeten, dan liggen de drie vijfhoeken plat, en ik neem aan dat dat niet de bedoeling is.
Dus moet er een hoek van 90° tussen passen.
Er zijn in principe drie mogelijke drievlakshoeken in de apenrots:
I: 120-120-90
II: 120-90-90
III: 90-90-90
Ik weet niet of elk van deze drie mogelijkheden ook daadwerkelijk voorkomt, maar type I in ieder geval wel (zie plaatje), en vanwege het totaal aantal hoeken van 90° (2 keer 18 is 36) en 120° (3 keer 18 is 48) moet tenminste een van de andere twee mogelijkheden ook voorkomen.
In elk hoekpunt komen 3 vijfhoeken bij elkaar (als je 'platte' hoeken niet toestaat). Er zijn dus (36+48)/3 = 28 hoekpunten.
Een mogelijke verdeling (maar ik weet niet of deze ook ruimtelijk te realiseren is):
20 hoekpunten van type I en 8 hoekpunten van type II
Je wilt nu dus de hoeken berekenen tussen de vlakken van elk van die drievlakshoeken.
Type II en III zijn simpel: daar zijn de hoeken tussen de vlakken 90°, 90° en 120°, respectievelijk drie keer 90°.
Type I is wat lastiger, maar het is te berekenen als je bedenkt dat dit type drievlakshoek ook voorkomt in een (afgeknotte) regelmatige piramide met grondvlak een vierkant, en opstaande ribben gelijk aan de zijde van dat vierkant. Lukt dat?
Om vervolgens van alle vijfhoeken de coördinaten van de hoekpunten te berekenen wordt nog een hele klus, maar ik hoop toch dat je een eindje op weg geholpen bent.
groet,

Anneke
13-8-2004