WisFaq!

Oppervlakte berekenen

De opppervlakte van het gebied, gelegen tussen de parabool y= x²-4, en de rechte door de oorsprong die de parabool snijdt in het punt (3,5), en hiervan het gebied aan de rechterkant van de y-as is;

Het antwoord is 10,5, maar kom er niet uit,

Wat ik heb;

Het gebied onder de x-as: primitieve functie:
-(¹/₃x³ -4x )
Het gebied boven de x-as: primitieve functie:
(5/6)x² - (¹/₃x³-4x)

Maar kom niet uit op 10,5, kunnen jullie mij misschien helpen? bedankt alvast!
Groetjes

Mirel
2-7-2004

Antwoord

Hieronder een situatieschets:

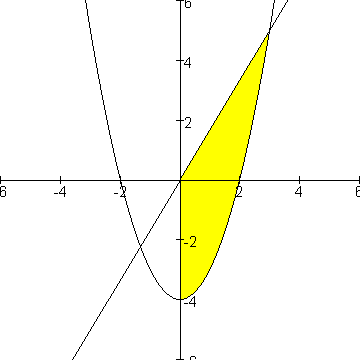
De parabool heeft als functievoorschrift: f(x)=x²-4.
De lijn heeft als functievoorschrift g(x)=⁵/₃x.
Omdat de lijn op het hele interval [0,3] netjes boven de parabool ligt hoef je niet op te splitsen in verschillende gebieden en kun je in dit geval gewoon
₀ò³(g(x)-f(x))dx uitrekenen.
Dit levert ₀ò³(⁵/₃x-(x²-4))dx=
₀ò³(⁵/₃x-x²+4)dx=
[⁵/₆x²-¹/₃x³+4x]₀³=
⁵/₆*9+¹/₃*27+12=10¹/₂

hk
2-7-2004