WisFaq!

Nulpunten bij een derdegraadsvergelijking

Hoe weet je of een derdegraadsvergelijking twee of drie snijpunten met de x-as heeft (wanneer er een is lukt me nog wel, dan is de discriminant van de afgeleide 0). Ik moet dit namelijk in een maplet zien te krijgen en dan kom ik volgens mij niet zo ver met ontbinden in factoren,

Marian
1-7-2004

Antwoord

Als een derdegraadsfunctie geen toppen heeft is er precies 1 nulpunt. Daarbij zou horen: de discriminant van de afgeleide is kleiner dan of gelijk aan nul.
Maar je mag dit niet omdraaien: ook als er twee toppen zijn (discriminant van de afgeleide groter dan nul) kan het zijn dat er maar 1 nulpunt is.
Neem bijvoorbeeld de functie f(x)=(x-3)(x²+2x+2).
In de grafiek hieronder is te zien dat deze functie 2 toppen heeft en toch maar 1 nulpunt.



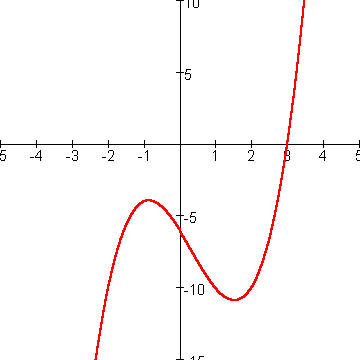
Gaan we nu de grafiek van deze functie verticaal omhoog schuiven dan krijgen we het volgende plaatje.



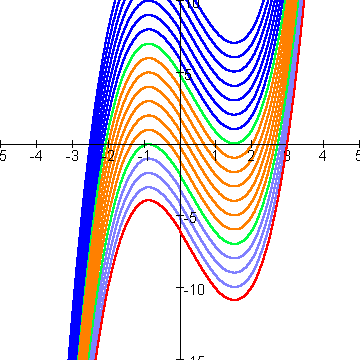
De linkertop komt steeds verder omhoog totdat de grafiek de x-as raakt in de linkertop. (de onderste groene grafiek). Er zijn dan 2 nulpunten.
Schuiven we nog iets verder omhoog (de oranje grafieken) dan zijn er 3 nulpunten.
Totdat de rechtertop op de x-as ligt: de andere groene grafiek. Er zijn dan weer 2 nulpunten. Schuiven we nog verder omhoog dan blijft er nog maar 1 nulpunt over.
In schema gezet krijg ik dan:

• Als er twee toppen zijn (discriminant afgeleide0), dan:
  • als de y-coordinaten van de toppen een verschillend teken hebben, de ene positief en de andere negatief =3 nulpunten
    kort gezegd ytop₁·ytop₂0: 3 nulpunten.
    
  • Een van beide toppen heeft y-coordinaat nul: 2 nulpunten.
    kort gezegd: ytop₁·ytop₂=0: 2 nulpunten.
    
• Alle overige gevallen: 1 nulpunt.

hk
1-7-2004