WisFaq!

Wortelvergelijkingen

Hallo, hier zijn we weer. Wij hebben laatst een paar vraagjes gesteld en hier komt er nog een. Onze probleemstelling is: hoe kun je een wortelvergelijking algebraïsch oplossen, die na 1 keer kwadrateren weer tot een wortelvorm komt. Hier hebben wij al een antwoord op. Maar hoe zit dit bij derdegraadswortelfuncties?

En dan nog een vraagje: waar is wortelvergelijkingen oplossen nou handig voor? Waar gebruik je dit voor in het dagelijks leven?

Met vriendelijke groet, Mirjam en Ilsalien.

mirjam en ilsalien
10-4-2002

Antwoord

Eigenlijk is het antwoord heel voorspelbaar. Je zult je vergelijking "tot de derde macht moeten verheffen". Maar dat is in het algemeen natuurlijk geen pretje en dat lukt dan ook eigenlijk alleen maar met tamelijk korte vergelijkinkjes.

Als voorbeeld: 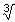x=x geeft al snel x=x³ en dat valt wel op te lossen. Je vindt x=0, x=-1 en x=1.

Maar neem nu eens 2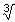x=x-4
De derde macht nemend krijg je 8x=(x-4)³.
En, als er niet een of andere toevalligheid ingebouwd zit in de som, is er maar één manier en dat is: het rechterlid helemaal uitwerken.

Maar, zelfs als je dat met frisse tegenzin gedaan zou hebben, dan nóg is het maar zeer de vraag of je een oplossing kunt vinden.

Kortom: derde graders zijn ondingen en over vierde, vijfde of nog hogere graders kun je maar beter zwijgen.

Tja, en wat het dagelijks leven betreft: in de wiskunde vindt men het nou eenmaal gewoon leuk om je krachten op dit soort dingen te beproeven. Of het nut heeft vraagt men zich helemaal niet eens af! Men wil gewoon kijken of het opgelost kan worden of niet. En, áls het niet oplosbaar is, dan willen ze ook nog eens weten waardoor dat dan komt.

Komt zo'n ingewikkelde vergelijking uit een bepaald onderzoek voort, dan kan men tegenwoordig met dure computerpakketten een oplossing laten benaderen (en ook dat lukt niet altijd!), op ongeveer de manier zoals je grafische rekenmachine het doet met intersection.

MBL
10-4-2002