Bekijk onderstaande tekening eens.
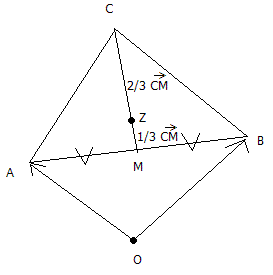
Ik heb maar één zwaartelijn (vanuit C op AB) getekend, die deelt AB middendoor (zie V-tekens). Verder is bekend dat de zwaartelijn in twee delen wordt verdeeld (door de andere niet-getekende zwaartelijnen) waarbij de delen zich verhouden als 2:1, oftewel één deel is 2/3 van CM (altijd bij het hoekpunt waar de zwaartelijn 'vertrekt') en het andere deel is 1/3 van CM.
De gekozen O is de oorpsrong die mag je willekeurig kiezen. Eerst gaan we de plaatsvector van m bepalen.
OA + AB = OB $\Rightarrow$ AB = OB - OA, en aangezien AM = 1/2AB geldt AM = 1/2(OB - OA). Dus OA + AM = OM $\Rightarrow$ OA + 1/2(OB-OA) = OM $\Rightarrow$ OM = OA - 1/2OA + 1/2OB $\Rightarrow$ OM = 1/2(OA+OB).
Verder is OM + MC = OC $\Rightarrow$ 1/2(OA+OB) + MC = OC $\Rightarrow$ MC = OC - 1/2(OA + OB) $\Rightarrow$ MC = OC - 1/2OA - 1/2OB.
Ook is OM + 1/3 MC = OZ $\Rightarrow$ OZ = OM + 1/3(OC - 1/2OA - 1/2OB)
$\Rightarrow$ OZ = 1/2OA + 1/2OB + 1/3OC - 1/6OA - 1/6OB
$\Rightarrow$ OZ = 1/2OA - 1/6OA + 1/2OB - 1/6OA + 1/3OC
$\Rightarrow$ OZ = 1/3(OA + OB + OC)
$\Rightarrow$ z = 1/3(a + b + c).
Groetjes,
Davy.
Davy
17-6-2004