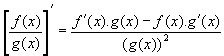
cos(x)∑cos(x)+sin(x)∑-sin(x))/cos2(x)=
moet worden
(cos(x).cos(x) - sin(x).-sin(x))/cos2(x)=(cos2(x)+sin2(x))/cos2(x)=1/cos2(x)
wl
16-6-2004
Ik heb jullie vanmorgen de vraag gesteld over het bewijs van de afgeleides van sin(x), cos(x) en tan (x). Jullie hebben daarop geantwoord dat ik bij tan(x) de quotiŽntregel moet gebruiken. Nu ben ik tot hier gekomen:
tan (x) = sin(x)/cos(x)
dan de quotiŽntregel toepassen
(cos(x)∑cos(x)+sin(x)∑-sin(x))/cos2(x)=
(cos2(x)-sin2(x))/cos2(x)=
-sin2(x)
Kunnen jullie mij aub helpen met de laatste stap(pen)???
Henk van Malsen
16-6-2004
Hallo Henk,
cos(x)∑cos(x)+sin(x)∑-sin(x))/cos2(x)=
moet worden
(cos(x).cos(x) - sin(x).-sin(x))/cos2(x)=(cos2(x)+sin2(x))/cos2(x)=1/cos2(x)
wl
16-6-2004
#25476 - Bewijzen - Leerling bovenbouw havo-vwo