Om 44x4 - 207x3 + 182x2 + 165x - 108 te kunnen ontbinden in factoren moet je eerst een nulpunt zien te vinden. Een nulpunt is een deler van de constante term, hier dus 108. De delers van 108 zijn ±1, ±2, ±3, ±4, ±6, ±9, ±12, ±18, ± 27, ±36, ±54 en ±108. Door een voor een 1, -1, 2, -2,... in de functie in te vullen kom je erachter welke een nulpunt is, want de functiewaarde is dan 0 (m.a.w. je vult een deler van de constante term in de functie, en de y-waarde is 0). 3 blijkt een nulpunt te zijn.
Wat je nu gaat doen is (x - nulpunt) alvast opschrijven, dus (x - 3). Om nu te weten met welke factor dit vermenigvuldigd moet worden, moet je de oorspronkelijke functie delen door x-3. Via een Euclidische deling (je zou ook het schema van Horner kunnen toepassen, maar dat schema ken je hoogstwaarschijnlijk niet, je zou eens kunnen zoeken in de Wisfaq-database).
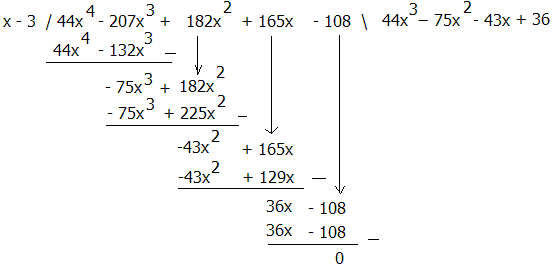
De rest is 0 (dus een opgaande deling) en bijgevolg is 44x4 - 207x3 + 182x2 + 165x - 108 = (x-3)(44x3-75x2-43x+36).
Misschien kunnen we die tweede factor ook ontbinden in factoren? We gaan dezelfde procedure uitvoeren: de delers van 36 zijn ±1,±2,±3,±4,±6,±9,±12,±18,±36. Wat je ook in 44x3-75x2-43x+36 invult, je komt géén functiewaarde 0 uit. Wat je wel zou kunnen doen is m.b.v. je GRM de nulpunten bepalen, dan krijg je bij benadering de punten -0,7992066283, 0,5146846891 en 1,989067394. De hoofdstelling van de algebra zegt dat een n-de graads veelterm altijd n (reële en/of complexe) wortels heeft, we hebben 3 oplossingen dus kan 44x3-75x2-43x+36 worden ontbonden in 44(x+0,7992066283)(x-0,5146846891)(x-1,989067394).
Groetjes,
Davy.
Davy
3-6-2004