WisFaq!

Hoe bereken ik de weg naar Mars?

U heeft verteld aan een ander persoon hoe je ongeveer de afstand van de aarde tot aan Mars kunt berekenen/meten. U zou hij/zij de moeilijke details besparen. Ik zou graag precies willen weten hoe je de weg kunt meten van de aarde tot aan Mars, het is voor mijn Praktische Opdracht voor school. Kunt U me helpen of kunt u mij een (Nederlandse)site geven waar dit staat uitgelegd?

Jean-Paul
2-6-2004

Antwoord

Twee waarnemers op aarde zien een planeet in verschillende richtingen. Het verschil noemt men de parallax.

De parallax is de tophoek van een gelijkbenige driehoek. Als je dan de afstand tussen de waarnemers weet kun je met behulp van de sinus de afstand van de waarnemer tot de planeet berekenen.

Het makkelijkste is als je precies aan de andere kant van de wereld gaat staan dan de andere waarnemer. Je krijgt dan namelijk: sin(p)=r/a met r is de straal van de aarde en a de afstand van de waarnemer tot de planeet.



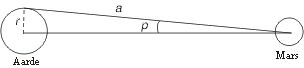
Omdat de afstand van de aarde tot de planeet nagenoeg gelijk is aan de afstand van de waarnemer tot planeet, kun je gerust zeggen dat a de afstand van de Aarde tot de planeet is.

Er geldt dus:

sin(p)=r/aÞa=r/sin(p)

Dit staat in het artikel 'Het meten van afstanden in het zonnestelsel'duidelijk en uitgebreid uitgelegd.

• Het meten van afstanden in het zonnestelsel

Met sterren kun je ook zo de afstand berekenen. Dat gaat zelfs nog iets mooier.

Bij het berekenen van de afstand tot een ster gebruikt men i.p.v. de straal van de Aarde de straal van de baan van de Aarde om de zon, of te wel de afstand van de Aarde tot de zon. Het grote verschil met de afstand meten tot een planeet is dat nu de zelfde waarnemer gewoon een half jaar moet wachten op zijn tweede waarneming en dan de parallax kan bepalen.



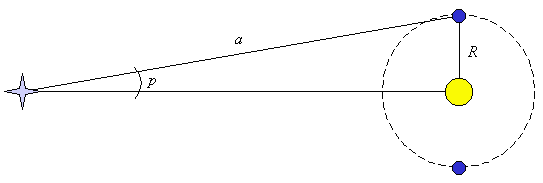
In het bovenstaande plaatje zie je weer dat geldt: sin(p)=r/a

Omdat bij hele kleine hoeken de sinus van een hoek in radialen gelijk is aan de hoek zelf. (Vul maar 0,00001rad in je rekenmachine in voor sin(p))

Omdat de parallax bij sterren heel klein is kunnen we zeggen dat:

p=r/a (p in radialen)

Omdat sterrenkundigen de hoek in boog seconden uit willen drukken moeten we het met 206265 vermenigvuldigen:

p=206265·r/a (p in boogseconden)

Voor de afstand kun je de eenheid AE gebruiken, dit is de afstand van de aarde tot de zon. En dat geeft dus:

p=206265·1/a

1 AE is in de sterrenkunde toch een wat kleine maat. Daarvoor hebben ze een andere eenheid, namelijk parallax-seconden (pc), bedacht die ongeveer gelijk is aan 206265AE.

Als we die gebruiken krijgen we de formule:

p=1/a (met p in boogseconden en a in parallax-seconde)Þ a=1/p

Hier nog twee links die dit uitleggen:

• Geometrische afstandsbepaling
• Afstand van sterren

Gerben
3-6-2004