WisFaq!

Oppervlakteberekening

Hallo!
Ik heb een groot probleem met de volgende opgave;
gegeven is de kromme y²=x²(2+x)/(2-x)
gevraagd is de oppervlakte van de lus (grenzen -2 en 0)
Los ik dit op met het type òy dx of moet het anders (bvb met poolcoördinaten of parametervergelijkingen of zo)?
Ik heb geprobeerd om te stellen dat de oppervlakte gelijk is aan 2 keer de oppervlakte van de positieve wortel.
Dan heb ik geprobeerd x gelijk te stellen aan 2cost zodat:
òxÖ(2+x)/(2-x) dx = ò2cost Ösin²t/(1-cost)² d(2cos t)
Zo is het wortelteken wel weg maar ik kan niet verder.
Alvast bedankt

Elke
26-5-2004

Antwoord

Beste Elke,

Als y²=x²·(2+x)/(2-x) dan is y=±Ö(x²·(2+x)/(2-x))
ofwel y=±xÖ[(2+x)/(2-x)].
Als we een plotje maken op het interval [-2,0] van de functies xÖ[(2+x)/(2-x)] en -xÖ[(2+x)/(2-x)] dan zien we

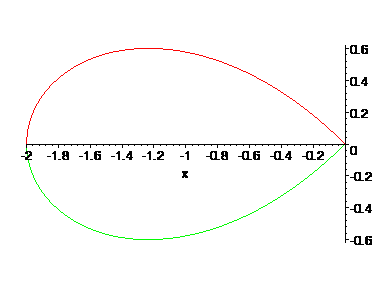
De bovenste grafiek is gespiegeld in de x-as, en dus is de oppervlakte van de totale grafiek gelijk aan 2 keer de integraal van de bovenste grafiek, dus de totale oppervlakte is 2·_-2ò⁰xÖ[(2+x)/(2-x)]dx.

Hoe je die integraal onbepaald moet oplossen staat hier beschreven, daarvan is onbepaald de uitkomst -2Ö(-x²+4)-0,5x·Ö(-x²+4)+2·arcsin(0,5x).
Dus bepaald (tussen de grenzen x=-2 en x=0) wordt dit 4 - p.

Maar dat is de oppervlakte van de grafiek boven de x-as, de oppervlakte van de grafiek onder de x-as is hetzelfde (oppervlakte is nooit negatief), dus ook 4 - p.

De totale oppervlakte is dan ook 2(4-p) = 8 - 2p, dus ongeveer 1,7168.

Davy.

Davy
28-5-2004