WisFaq!

Re: Ruimtediagonalen en een afgeknotte kubus

L³ - (8x inhoud piramide) is dan de inhoud piramide.
Inhoud van zo'n piramide = ¹/₃ · opp grondvlak · hoogte.
Dus 1/3.(xwortel(2).h/2).H met h is hoogte grondvlak en H hoogte piramide.
Ben ik nu juist bezig? En hoe moet het dan verder? Ik vind deze beide hoogtes niet en het mag enkel in functie van L zijn...

eddy
26-5-2004

Antwoord

De formule voor de inhoud van die piramides zie ik toch niet.



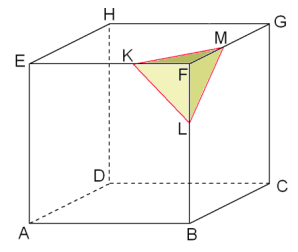
Neem als grondvlak van de piramide een driehoekje als DKFM en als hoogte de lengte van het lijnstukje FL. Ga na dat dat klopt!

Hoe bereken je nu de oppervlakte van dat driehoekje en de lengte van dat lijnstukje? (zie figuur hieronder met iets andere letters dan hierboven)



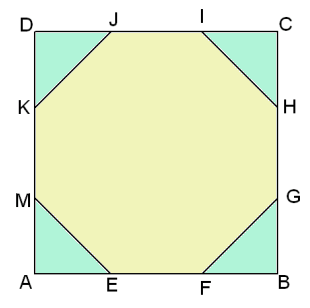
AB=L
EF=FG=GH=... enz...

Neem FB=x en pas de stelling van Pythagoras toe in DFBG.
Gebruik: FG=EF, dus FG=L-2x

Er geldt: x²+x²=(L-2x)²

Hiermee kan je x uitdrukken in L. Daarmee kan je de oppervlakte van het grondvlak uitdrukken in L en ook de hoogte uitdrukken in L en daarmee kan je dan de inhoud van één zo'n piramide uitdrukken in L. En dan ben je toch al een eind op weg...

WvR
26-5-2004