WisFaq!

Vectoren

Construeer voor een parallellogram ABCD het punt E zo dat DE=BD. Wat is het punt D voor de driehoek ACE? Geef een bewijs.

Het punt construeren is geen probleem. Ik zie wel dat het punt D het zwaartepunt is van de driehoek maar kan het niet bewijzen. Ik kan wel bewijzen dat D op 2/3 ligt van punt E op de zwaartelijn van E naar AC, maar hoe het verder moet zie ik niet.

Jim Van Leemput
22-5-2004

Antwoord

Beste Jim,

Ik heb het punt E op het verlengde van de diagonaal BD gekozen.

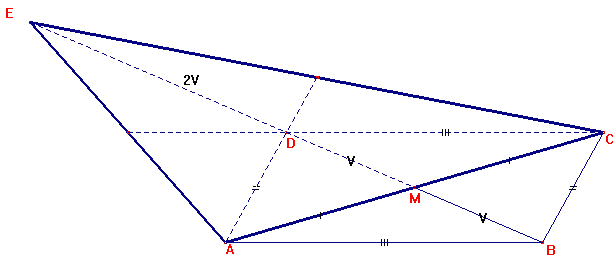
Je weet dat de diagonalen in een parallellogram elkaar middendoor delen, dus |AM| = |MC| én |MD| = |MB|. Omdat |DE|=|BD| en |BD|= V + V = 2V moet gelden dat |DE|=2V. Vanuit E wordt de diagonaal in M middendoor gedeeld (dit was het snijpunt van de diagonalen al, vandaar dat ik het punt E op lijn BD heb getekend).
Dus |EM| is al de zwaartelijn vanuit E, maar we weten ook dat |DM| zich tot |ME| verhoudt als V:(V+2V) = V:3V ookwel 1:3, en dat |DE| zich verhoudt als 2:3 (namelijk 2V:3V). Dus D is het zwaartepunt.

Groetjes,

Davy.

Davy
22-5-2004