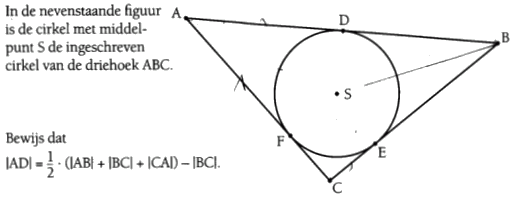
Je kan er toch maar enkel van uitgaan dat |SF|=|SE|=|SD| omdat het middelpunt van de ingeschreven cirkel even ver ligt van de zijden.
Bram M
20-5-2004
Zou u mijn kunnen helpen met te bewijzen dat |AD| = (1/2)*(|AB|+|BC|+|CA|)-|BC|
Je kan er toch maar enkel van uitgaan dat |SF|=|SE|=|SD| omdat het middelpunt van de ingeschreven cirkel even ver ligt van de zijden.Bram M
20-5-2004
Beste Bram,
Gelukkig is het vrij gemakkelijk. Je moet je alleen realiseren dat bijvoorbeeld |AF| en |AD| gelijk zijn. Aangezien AS een symmetrie-as is van de figuur van de cirkel samen met punt A, moeten AF en AD in deze lijn spiegelbeelden van elkaar zijn, en dus even lang. Trouwens, ook via de Stelling van Pythagoras is dit goed in te zien. AFS en ADS zijn rechthoekige driehoeken met een samenvallende zijde AS en met |FS|=|DS|, waarna AF en AD door berekening even lang blijken.
Nu moet het lukken!
FvL
22-5-2004
#24255 - Vlakkemeetkunde - 2de graad ASO