WisFaq!

Oppervlakte met bepaalde integralen

Hoi wisfaq,

Ik heb een vraagje,

Bereken de opppervlakte van het lensvormige deel van het vlak gelegen tussen de cirkels met vergelijking x²+y²=1 en x²+(y-1)²=1

Ik weet niet goed hoe te beginnen :/

thx op voorhand.

tjer
11-5-2004

Antwoord

Noem f(x) = Ö(1-x²) de functie van het bovenste gedeelte van de eerste cirkel.
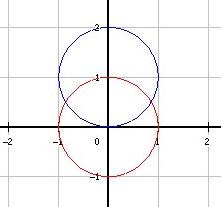
Noem g(x) = 1 - Ö(1-x²) de functie van het onderste gedeelte van de tweede cirkel.
Bepaal hun snijpunten (x = -^Ö3/₂ en x = ^Ö3/₂).

Bereken nu de oppervlakte O₁ tussen f(x), x-as en de 2 grenzen.
Bereken de oppervlakte O₂ tussen g(x), x-as en de 2 grenzen.
De gevraagde oppervlakte = O₁ - O₂.

LL
11-5-2004