WisFaq!

Priemgetallen

allereerst even een makkelijk vraagje.
Een getal n$>$1 is priem als hij geen delers d bezit met 1$<$d$<$=√n. Met een voorbeel is het logisch maar hoe kun je dit bewijzen? vooral als n oneindig is?
Ik kan ook dit bewijs niet leveren waarom er oneindig veel priemgetallen p $\equiv$ 1 mod 4 bestaan.
Wel dat er oneindige priemgetallen p $\equiv$ 3 mod 4 bestaan. Namelijk zo:
we kunnen voor ieder n-tal priemgetallen p₁,p₂,...,pn het getal N=4(p₁p₂...pn)²-1 vormen. Omdat N congruent is met 3 mod 4 kunnen niet alle priemdelers van N congruent zijn met 1 mod 4. Bovendien is N niet door de priemgetallen pi deelbaar. Er is dus een priemgetal p $\equiv$ 3 mod 4 buiten ieder voorgegeven n-tal priemgetallen. Dit impliceert dat er oneindig veel priemgetallen congruent met 3 mod 4 zijn. Is dit bewijs trouwens goed?
en dan nog iets. de getallen p₁p₂p₃...pn+1 met p₁,p₂,..pn priem, zijn die getallen dan ALLEMAAL priem? nee toch?
alvast bedankt adrian

adrian
17-4-2004

Antwoord

1) Stel n niet priem met een echte deler d$>$√n dan geldt n=d·e waarbij e een echte deler is met e$<$√n. Bijgevolg hoef je alleen naar delers te zoeken t/m de waarde √n om te concluderen dat een getal priem is.

2) voor het bewijs van het oneindig zijn van de verzameling priemgetallen van de vorm 3 mod 4 ga je als volgt te werk.
·wanneer een getal de vormt heeft van -1 mod 4 dan heeft hij minstens een deler van deze vorm
·zij m $\in$$\mathbf{N}$⁺ Beschouw G = 4m!-1 Laat nu zien dat elke priemdeler van G $>$ m is.
Dat betekent dat je volgens mij dat kwadraatje dus niet nodig hebt.

3) Het aantal priemgetallen van de vorm 1 mod 4 is ook oneindig maar op dit moment zie ik het bewijs niet helemaal zitten.

4) De getallen p₁p₂p₃...pn+1 met p₁,p₂,..pn priem ALLEMAAL priem?? Nee hoor, zelfs bijna allemaal niet priem (als al die priemgetallen oneven zijn). Wel kun je hieruit een nieuwe priemdeler vinden volgens de stelling van Euclides.

Toch nog wat gevonden voor 3...... voor wat het waard is.


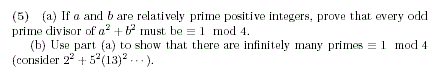
Met vriendelijke groet

JaDeX

jadex
18-4-2004