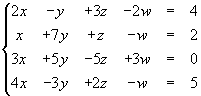
Je moet nu één van de variabelen in het stelsel elimineren zodat je nog maar een stelsel hebt met 3 variabelen. Dit herhaal je totdat je nog maar 1 variabele hebt.
Om dit te bereiken moet je twee vergelijkingen nemen en daar een variabele elimineren. Dit doe je drie keer met verschillende paren vergelijkingen.
Je krijgt dan drie vergelijkingen met 3 variabelen. Maar let op! gebruik
in elk paar steeds één de zelfde vergelijking. Het is het handigste als
je deze uitgebreide tussenstap uit je hoofd doet met eventueel een rekenmachine,
maar ik doe er één uitgebreid voor.
Als eerst schrijf ik de vergelijkingen in een iets andere volgorde op. Ik zet de
vergelijking die ik in elk 'paar' gebruik onderaan in het stelsel:

Nu vermenigvuldig ik de onderste vergelijking steeds met een getal zodat ik de
zelfde factor met x heb bij twee vergelijkingen. (soms is het handiger om
beide vergelijkingen met een getal te vermenigvuldigen, anders krijg je rare
breuken). Dan trek ik de onderste vergelijking van de andere af (mag ook
andersom).
Dit gaat zo bij de onderste twee vergelijkingen:
Doe dit nu ook voor eerste en de laatste en de tweede en de laatste. Je
krijgt dan het volgende stelsel:
Het vervolg gaat eigenlijk weer het zelfde. Merk op dat het nu slimmer is om de
eerste vergelijking mee te nemen en in de onderste twee vergelijkingen w
te elimineren. Je mag de eerste gewoon meenemen, want wanneer je de onderste
vergelijking met nul vermenigvuldigd en hem dan van de eerste vergelijking
aftrekt krijg je de zelfde vergelijking weer terug.
Je krijgt dan het volgende stelsel:
Laatste keer:![]()
We hebben nu één variabele gevonden en nu is het invullen geblazen!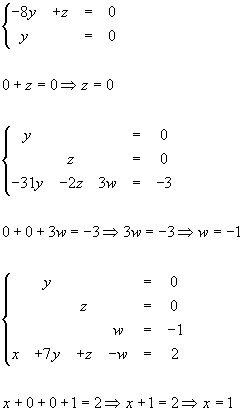
Hier kun je een programma genaamd 'LiVe' vinden. Het is wel een leuk programma, maar het werkt (tijdens de tussenstappen) niet exact.
Gerben
4-4-2004