De stelling van Thales die jij bedoelt (zoals je toelichtte), is de volgende:
Voor een punt P op de cirkel met middellijn AB geldt: $\angle$APB = 90°.
En omgekeerd:
Als $\angle$APB = 90°, dan ligt P op de cirkel met middellijn AB.
Tja, wat kun je er mee?
Wat Thales er mee gedaan heeft, is slechts een kwestie van gissen. Het enige dat we ervan weten is (citaat uit Heath: A History of Greek Mathematics):
According to Pamphile's (Pamphila was een Griekse vrouwelijke filosoof/meetkundige; ze leefde omstreeks 60 na Chr.; dk) evidence, quoted by Diogenes Laertius, Thales also inscribed a right-angled triangle in a circle.
Diogenes Laertius quotes the following passage:
'Pamphile says that Thales, who learnt geometry from the Egyptians, was the first to describe on a circle a triangle
(which shall be) right-angled, and that he sacrificed an ox (on the strenght of the discovery). Others, however,
including Apollodorus the calculator, say that it was Pythagoras'.
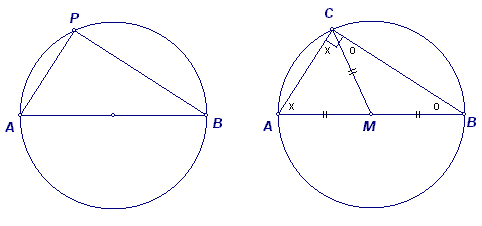
Mogelijk dat Thales 'zijn' vondst gebruikte bij zijn astronomische berekeningen (hij voorspelde naar alle waarschijnlijkheid de zonsverduistering van 28 mei (?) 585 v. Chr).
Maar hij zou er meer mee hebben kunnen doen.
Immers, Thales wist ook dat de basishoeken van een gelijkbenige driehoek gelijk zijn (opnieuw een 'stelling van Thales'). Dan zou hij met die kennis hebben kunnen bewijzen (evenals wij nu), dat de som van de hoeken van een driehoek gelijk is aan 180° (gelijk aan twee rechte hoeken, schreven ze toendertijd).
Lukt jou dat (kijkend naar de figuur hierboven, rechts)?
En wat nog meer?
In de eerste plaats is deze stelling van Thales belangrijk voor de meetkunde zelf.
We kunnen 'em gebruiken bij het bewijs van andere stellingen.
Bijvoorbeeld.
Als van een driehoek de zwaartelijn (uit een hoekpunt) naar een zijde gelijk is aan de helft van die zijde, dan is de hoek in dat hoekpunt een rechte hoek.
Het bewijs van die stelling laat ik aan jou! (Zie weer de figuur hierboven, rechts.)
Verder is de stelling zeker van belang voor de verdere uitbouw van de meetkunde.
De stelling vormt de basis voor de zogenoemde koordenvierhoeken (vierhoeken waarvan de hoekpunten op een cirkel liggen).
Kijk maar eens naar de volgende tekening.
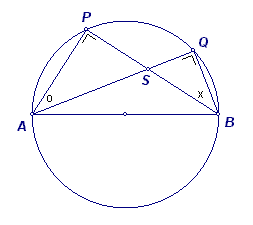
We weten dat APB = 90° en dat AQB = 90°.
De punten A, B, Q en P liggen dan op een (Thales-)cirkel. De zijden van de vierhoek ABQP (QP is niet getekend) zijn koorden van die cirkel.
Daarom heet ABQP koordenvierhoek.
En daaruit kunnen we dan weer een bijzondere eigenschap van zogenoemde omtrekshoeken afleiden:
Bewijs dat PAQ = PBQ (omtrekshoeken op dezelfde boog zijn gelijk).
(Nb. Voor het bewijs kan je ook een stelling gebruiken die naar Thales genoemd is: overstaande hoeken zijn gelijk!)
En tenslotte. Je kan, op basis van de stelling van Thales, zonder passer, een groot aantal punten van de cirkel
met middellijn AB construeren.
Zie de volgende Cabrijavapplet.
We gaan uit van twee vaste punten A en B.
Met het punt
 Natuurlijk kan je hetzelfde doen met je geodriehoek!
Natuurlijk kan je hetzelfde doen met je geodriehoek!Enneh, denk aan de bronvermelding in je PO: WISFAQ!
dk
29-3-2004