WisFaq!

Uitleg over parametervoorstelling van de torus

Bij de parametervoorstelling van de torus, werken we met 2 hoeken,(in onze cursus staat: de poolhoek van de straal en de poolhoek van de afstand c (wanneer we de cirkel om een as laten wentelen die zich op een afstand c van het middelpunt van deze cirkel bevindt).
Maar ik kan me eigenlijk deze hoeken niet goed voorstellen... Kunnen jullie mij misschien hierbij helpen?
Alvast héél hard bedankt,
groetjes
Caro

Caro
23-3-2004

Antwoord

Bekijk eerst even de twee onderstaande figuren. De bovenste figuur geeft de cirkel weer die moet worden gewenteld om de z-as. De tweede figuur toont die wenteling.



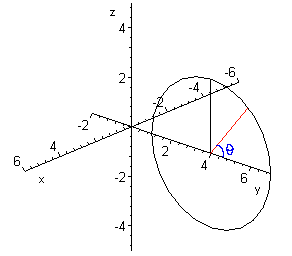
We stellen eerst de parametervoorstelling op van de cirkel. Deze cirkel ligt in het YZ-vlak dus de x-coördinaat van de parametervoorstelling is al nul. Je weet waarschijnlijk wel dat een cirkel in het YZ-vlak met middelpunt in de oorsprong een parametervoorstelling [0,r*cos(q),r*sin(q)] heeft. In ons geval ligt het middelpunt niet in de oorsprong, maar stel in het punt y=a. Dan wordt de parametervoorstelling [0,r*cos(q)+a,r*sin(q)], maw, alle punten van de cirkel met middelpunt in de oorsprong worden met a naar rechts verschoven over de y-as. Je krijgt nu de cirkel die afgebeeld staat op figuur 1. Merk op dat de q op de figuur overeenkomt met de poolhoek van de cirkel indien hij zijn middelpunt in de oorsprong had gehad.

ter herinnering: De parametervoorstelling van de cirkel is
[0,r*cos(q)+a,r*sin(q)] met r de straal van de cirkel, en a de coördinaat van het middelpunt. (q loopt tussen 0 en 2p)

Nu willen we deze parametervoorstelling wentelen om de z-as. Hiervoor bestaat een eenvoudig trucje uit de matrixrekening. Waarschijnlijk kan je wel twee matrices met elkaar vermenigvuldigen.
Om je parametervoorstelling te wentelen om de z-as moet je de parametervoorstelling rechts vermenigvuldigen met de matrix:


(analoog voor wentelingen van krommen om de x as: vermenigvuldig je parametervoorstelling van je kromme met de matrix:


en voor wenteling om de y-as:


f loopt overal tussen nul en 2p om een volledige omwenteling te bekomen (2p=360°)

Werken we de matrixvermenigvuldiging uit (neem de eerste matrix want het is een wenteling om de z-as)
dan bekomen we de parametervoorstelling:

[-sin(f)*(a+r*cos(q)) , cos(f)*(a+r*cos(q)) , r*sin(q)] met 0f2p , 0q2p

Je ziet de hoek f lopen in de tweede figuur.

Dus in deze parametervoorstelling bepaalt q de poolhoek van de cirkel indien zijn middelpunt in de oorsprong had gestaan, en f bepaalt de omwenteling.
(deze hoeken worden in tegenwijzerin gebruikt. Dit is de afspraak voor geöriënteerde hoeken).

Ik hoop dat het een beetje duidelijker geworden is.

Koen Mahieu

km
24-3-2004