WisFaq!

Logschaal omzetten in formule

Ik heb op een A4-tje 3 log schalen naast elkaar staan. Toegelicht: zoiets als :



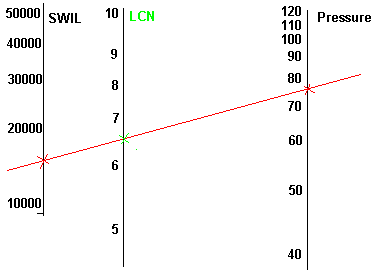
Alle de schalen zijn logaritmisch. De tekening heb ik snel met behulp van paint ter illustratie nagetekend. Dus geen werkelijke tekening. Die heb ik helaas niet, digitaal
Weet ik een waarde van as 1 en 2 dan kan ik door een rechte lijn te trekken waarde op as 3 aflezen.

Doel:
Nu wil ik dit omzetten in een formule. (Log-waarde per as omzetten in een cm waarde en dan is het goed om met verhoudingen (hoeken en afstand) de 3de waarde te achterhalen.)

Probleem:
Hoe kan ik een log Y-as omzetten naar een formule Y=a·g^x
(zonder a g en x te moeten schatten en uitproberen.)

concreet:
Dit is mijn vraag:
Y is waarde op logaritmische as (bijv de druk in PSI).
X is waarde in cm. (ligt op de Y-as maar dan met een ander referentiekader ook wel een secundaire as genoemd))

Mijn vraag is:
Is er een methode dat ik een waarde op de logaritmische as in een formule kan uitdrukken in cm.
dus en visa versa. Y=F(X)

Stel Y is waarde op linieare as (bijv de druk in PSI).
Vraag wat is Y=F(X)?
Dan zou de methode zijn
Bepaal 1 waarde op de as bijv.
Y= 1 PSI
Meet de waarde in cm
Y = 0,5 cm
Verhouding tussen beide is 1/0,5= 2
De formule zou zijn
Y(psi)= 2 X(cm)
EEN EENVOUDIGE METHODE

Het probleem waar ik nu mee zit is dat de as niet lin. maar een log. schaal heeft.
dus meer variabelen:
- grondtal is onbekend,
- eventuele verhoudingsfactor

Op mijn log. as staan de volgende waarde met een liniaal heb ik de waarden in cm opgemten
Y X(cm)
10.000 0
11.000 0,58
12.000 1,09
13.000 1,55
14.000 1,98
15.000 2,4
16.000 2,78
17.000 3,1
18.000 3,48
19.000 3,8
20.000 4,1

Wat is de formule?
En welke methode heb je gebruikt (Hoe ben je tot de formule gekomen)?

jeroen
23-3-2004

Antwoord

Beste Jeroen

Ik heb geen goed beeld van je voorkennis, dus het kan zijn dat ik te grote (of te kleine) stappen maak.
Ik gebruik de tabel die je gemaakt hebt
Als je X 4,1 groter maakt wordt Y 2 maal zo groot
Daarom is het handig een nieuwe schaalverdeling te maken:
je deelt al je gemeten waarden door 4,1. De uitkomst noem ik Z
Bij Z=0 hoort dus Y=10 en bij Z=1 hoort Y=20
Dus Y=10·2^Z
Omdat geldt Z=X/4,1 kun je ook schrijven Y = 10·2^X/4,1
Dit kun je gebruiken om afgelezen cm om te zetten in werkelijke waarden. De omgekeerde richting gaat met de log
Ik gebruik eerst weer Z.
We hadden 10·2^Z= Y
Dus 2^Z= Y/10
Dus Z = ²log (Y/10)
Dus Wanneer je weer voor Z invult: X/4,1 krijg je :
X/4,1 = ²log (Y/10)
Dus X = 4,1 · ²log (Y/10)

Op de zelfde manier kun je formules maken voor de andere schalen.
Dan is het nog wel wat werk om de gewenste formule voor het verband tussen de drie grootheden te vinden, maar dat is deel 2.
Kijk eerst eens of je met bovenstaande verder kan.
Als er iets niet helemaal helder is lees ik het graag

gk
29-3-2004