wat hiermee wordt bedoeld? Ik neem aan dat je wel weet wat regressie is. Doorgaans heb je een gewone puntenwolk en dan trekt men er een regressielijn door. Bij de methode van de kleinste kwadraten is dan de som van de afstanden van elk punt in het kwadraat tot aan de regressielijn minimaal. Dit geeft doorgaans een goede benadering, maar niet altijd. Bijvoorbeeld bij tijdreeksen loopt het wel eens fout. Met een tijdreeks bedoel ik dat op de X-as een periode staat (vb periode 1980-2000) en dan voor elk jaar de desbetreffende waarde op de Y-as. Een goed voorbeeld hiervan is het bruto binnenlands product tijdens een bepaalde periode. Zo'n tijdreeks heeft bijna steeds als eigenschap dat ze de neiging heeft om jaarlijks procentueel te stijgen (doorgaans dus een exponentiŽle functie).
Als concreet voorbeeld heb ik een tijdreeks genomen van een spaarrekening. In 1980 heb je er Ä 1000 op gestort en elk jaar brengt het 10% op. De puntenwolk ziet er dan als vlogt uit:
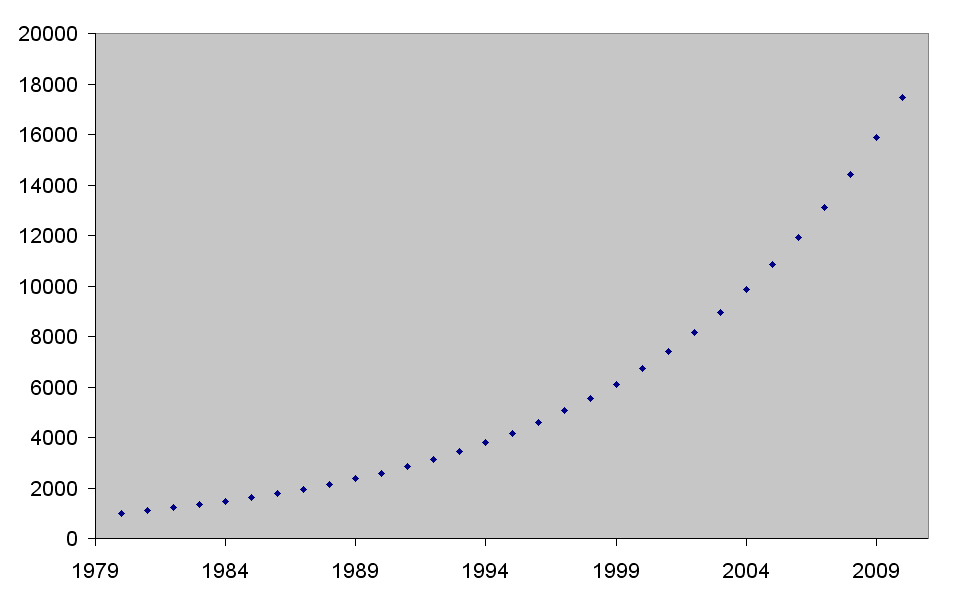
We kunnen hier dan een lineaire regressie van maken.
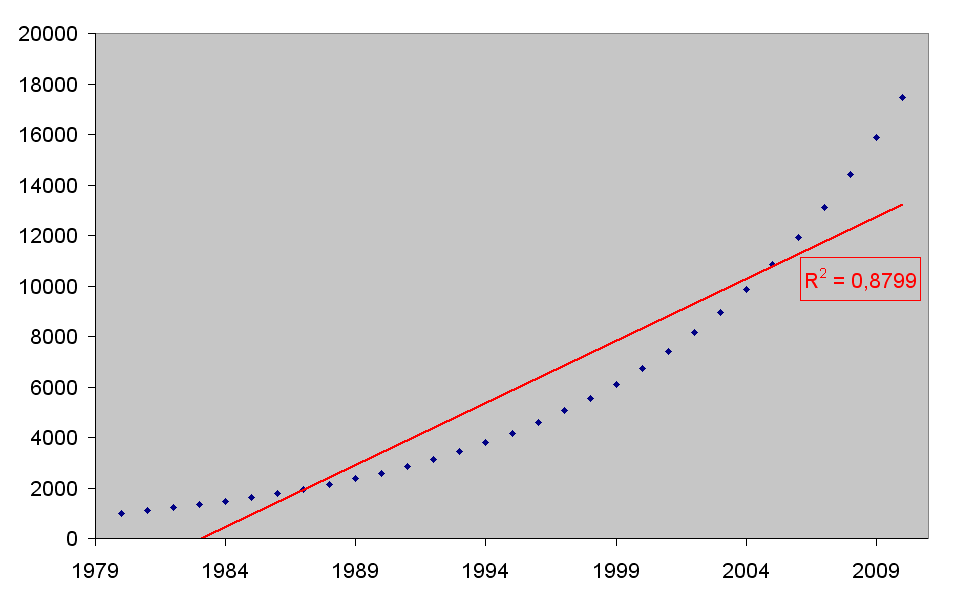
Je ziet nu zelf dat 2 punten op de regressielijn liggen, maar dat de meeste punten er vrij ver van verwijderd liggen. R2 = 0,8799 wat eigenlijk nog wel meevalt. Alleen is het zo dat je bij regressie niet noodzakelijk een lineair verband moet nemen, soms benadert een exponentieel of logaritmisch verband beter de werkelijkheid. Laten we eens een exponentiele regressie nemen, omdat het hier om een exponentiŽle functie gaat.
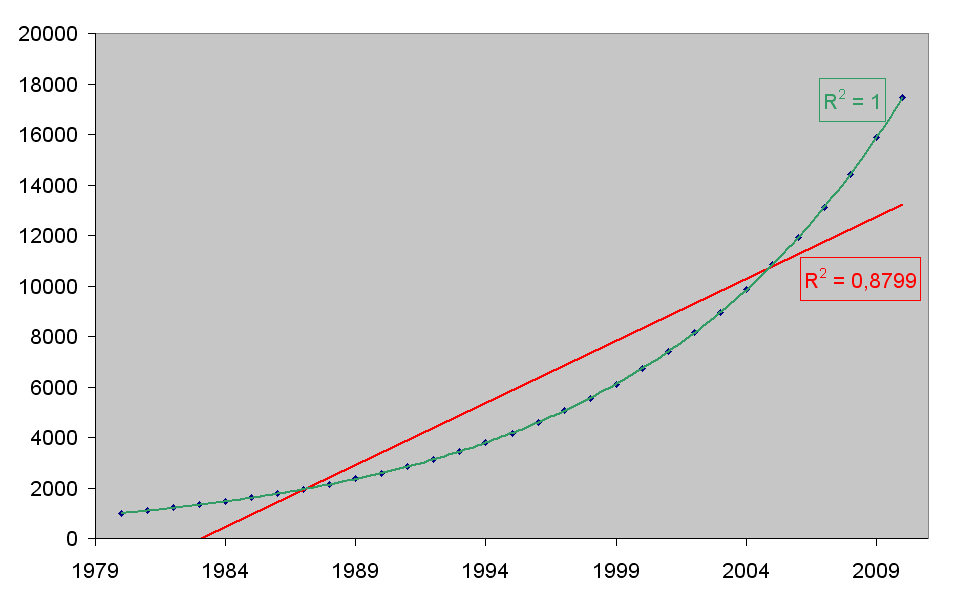
Dit is heel wat beter, nietwaar? Alle punten liggen op de regressielijn. R2 is dan ook 1. Nu, er zijn nog situaties waar je best geen lineair verband gebruikt. Ik heb je al op weg gezet, denk even na, en je zal nog wel situaties vinden.
Groetjes,
tg
24-3-2004