Ik zit in het vierde jaar van de havo ik ben nu bij een thema waar ik echt geen bal van snap.
Ik denk dat u mij wel kunt helpen.
Ik heb wat vragen / opdrachten hieronder vermeldt die we nu krijgen, kunt uw me helpen met het oplossen van deze moeilijke opdrachten?
[0,2pi] is het interval.
=
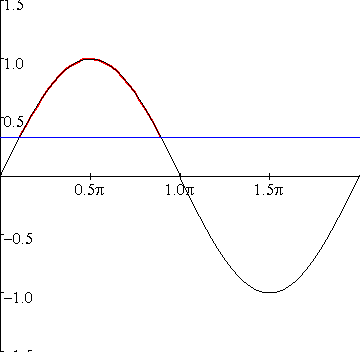
 sin x = sin 1
sin x = sin 1los x op
[o,4pi]
sin x
 -0,1
-0,1ook weer los x op
sin x = -0,246
En ook: Werk met y= sin x en dan wordt gesteld voor welke waarden van x geldt : sin x
 1/3.
1/3.Kunt u mij helpen bij het correct opschrijven van deze dingen.
Hartelijk dank.
Tom van Velde
8-3-2004
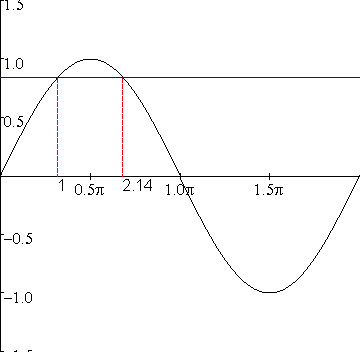
 2,14.
2,14.