Tja, als je die stelling niet mag gebruiken, dan wordt het een stuk creatiever, dat wel.
Laten we (3) even onder de loep nemen.
Je kunt hier teller en noemer vermenigvuldigen met een factor, waardoor die sinus van de halve hoek in het kwadraat komt te staan, en dus mooi vervangen kan worden door een cosinus.
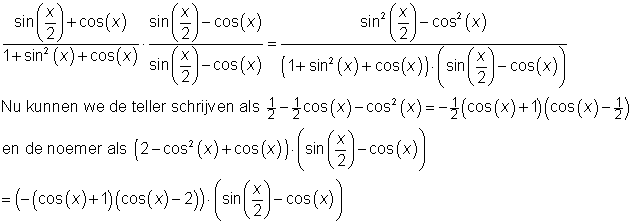
Nu kun je de boosdoener (cos(x) + 1) wegdelen uit teller en noemer, en vervolgens kun je $\pi$ zo invullen.
Dan nummer (4).
Vervang hier x - $\pi$/2 door y.
Dan wordt sin(x) = sin(y + $\pi$/2) = cos(y)
en cos(x) = cos(y + $\pi$/2) = -sin(y)
waardoor de limiet overgaat in de standaardlimiet y/sin(y) voor y$\to$0.
Ook de andere limieten vereisen meer creativiteit. Ik hoop dat je even verder kunt.
succes,
Anneke
8-3-2004