WisFaq!

Algemene formule brandpunt en richtlijn (2)

In een willekeurige parabool $f(x)=ax^2+bx+c$ is $\eqalign{-\frac{b}{2a}}$ inderdaad de x-coordinaat van het brandpunt dat op een denkbeeldige lijn door de top van de parabool ligt.

Hoe krijg ik $\eqalign{y=\frac{-1-b^2}{4a}+c}$ voor de richtlijn?
alvast bedankt.

Navin
17-3-2002

Antwoord

We willen een 'algemene' formule afleiden voor het brandpunt en richtlijn van een willekeurige parabool met vergelijking:

y=ax²+bx+c

We kijken eerst naar y=ax². Daarvan kennen we het brandpunt en de vergelijking van de richtlijn

• Brandpunt en richtlijn van een parabool

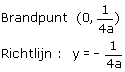
Nu is y=ax²+bx+c precies dezelfde parabool als y=ax², alleen verschoven met de vector (x_top,y_top).

De coördinaten van de top die kennen we wel

• De coördinaten van de top berekenen

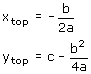
Daarmee kan je de volgende formules afleiden:


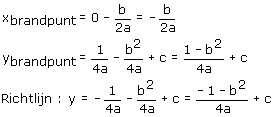
Waarmee de formules van Algemene formule brandpunt en richtlijn hebben afgeleid.

WvR
18-3-2002