WisFaq!

Inhoud van ruimtelichamen

Hallo,

Ik was bezig met het instuderen van een hoofdstuk dat over oppervlakte en inhoud van ruimtelichamen gaat. Ik heb verschillende oefeningen gemaakt , maar toch zijn er enkele oefeningen die ik niet begrijp , of niet kan afkrijgen. Ik hoop dat jullie me kunnen helpen. Ik heb het morgen nodig om te leren. DANK U .

1) I1,I2,I3 stellen de inhouden voor die ontstaan door het wentelen van een rechthoekige driehoek om de schuine zijde en de rechthoekszijden. BEWIJS ; 1/I1 = 1/I2=1/I3.

-- Ik heb alles zelf eens geprobeerd en uiteindelijk kom ik uit(ik werk met driehoek abc) : 1/3pa²b voor I2 , 1/3pb²a voor I3 en 1/3ph²c voor I1. Dus
eigenlijk geldt dan ook ; a²b = b²a= h²c(-- Te bewijzen)
MAAR DAN KAN IK NIET VERDRER , misschien ben ik fout bezig , maar ik weet het echt niet.

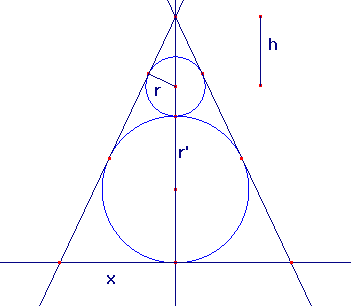
2) Gegeven zijn bollen å(m,r) en å(m',r'), met ongelijke stralen r en r',die mekaar uitwendig raken. We beschouwen de kegel welke omgeschreven is aan beide bollen. BEpaal de inhoud van het lichaam dat door deze oppervlakken begrensd wordt.

3) en een laatste vraag( misschien te veel gevraagd, maar ik wil het echt goed begrijpen en daarom ga ik een stukje ervan vragen en niet de vraag(opgave) zelf.) Als ik een kubus |efgh|
|abcd|
heb met ribbe 6. EN er zit hier een viervlak fach in. Hoe kan ik de hoogte van deze viervlak berekenen.

IK ZOU ECHT HEEL BLIJ ZIJN als ik hier een snelle antwoord op kan krijgen. Ik heb vrijdag test en die moeilijkere oefeningen wil ik ook graag doorhebben?

JULLIE zijn alvast BEDANKT.

Naïl
18-2-2004

Antwoord

Dag Naïl,

Die eerste opgave klopt niet: die inhouden zijn echt niet aan elkaar gelijk. Kijk de opgave nog eens goed na, misschien wordt er iets anders bedoeld.
Dan de bollen.

Vanwege de gelijkvormigheid geldt:
h/(h+r+r') = r/r'
dus h = r·(r'+r)/(r'-r)
Verder geldt (weer vanwege gelijkvormigheid):
x/(h+r+r') = r/Ö(h²-r²)
Hiermee kun je dus x uitdrukken in r en r'.
Daarmee heb je voldoende gegevens om de inhoud te berekenen.
Dan de laatste vraag: kijk eens op tetrahedron, daar vind je (tamelijk onderaan) de gewenste uitleg over een viervlak in een kubus.
succes!

Anneke
19-2-2004