WisFaq!

Samengestelde intrest met maandelijkse stortingen

Op een bankrekening wordt maandelijke 1% rente gegeven over het saldo, en per kwartaal 2,5% over het laagste saldo in dat kwartaal.
Per maand wordt er een x bedrag gestort.
Het beginsaldo bedraagt 0.
Hoe bereken je het saldo, met samengestelde intrest per jaar? En belangrijker hoe bereken je wat het eindsaldo is na een looptijd van 15 jaar, er van uitgaande dat er geen tussentijdse opnames zijn.

John van der Vuurst
16-2-2004

Antwoord

Beste John,

met volgende formule zou het moeten lukken:



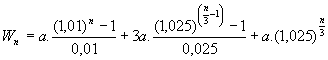
Met: W_n = waarde na n maand
a = maandelijks te storten bedrag

Hetgeen erachter zit, zijn de normale annuïteitenformules waarover je hier op Wisfaq genoeg vindt. Het eerste deel is de formule voor de eindwaarde bij 1%. Het tweede deel bekijkt de 2,5% over het laagste saldo in dat kwartaal.

Laten we dat eens bekijken. Elke maand wordt een bedrag a gestort, het bedrag op de rekening is dan:
maand 1 : a
maand 2 : 2a
maand 3 : 3a
laagste kwartaal 1: a
maand 4 : 4a
...
laagste kwartaal 2: 4a

Doen we zo verder dan zijn de laagste bedragen respectievelijk a, 4a, 7a, 10a.
Algemeen: laagste kwartaal n = a((n-1)*3 + 1)
Het probleem is dat we deze notatie moeilijk kunnen gebruiken in de annuïteitenformules. Daarom heb ik het vereenvoudigd door steeds 1 a eruit te halen. De rij wordt dan 0, 3a, 6a, 9a. In de formule kunnen we dan werken met 3*a en negeren we tevens het eerste kwartaal.

We moeten dan nog wel corrigeren voor het weghalen van 1*a tijdens elke maand en het laten vallen van het eerste kwartaal. Dit berekenen we via de laatste term.

Als je het bedrag wil weten na x jaar, dan moet je voor n 12*x invullen, dus na 1 jaar vullen we 12 in. We krijgen dan als waarde na 12 maanden bij een maandelijkse storting van bvb € 100: 1268,25 + 110,38 + 922,6875 = 2301,3175. Dit is vrij veel, want voor een gestort kapitaal van 1.200 krijgen we € 1101,3175 intrest. Zo'n bankrekening wil ik ook. Ben je zeker dat ze maandelijks 1% intrest geven en niet jaarlijks?

Groetjes,

tg
19-2-2004