WisFaq!

Formule van Cardano

Ik heb voor de oplossing van cardano gekeken bij

Zie Typen derdegraadsvergelijkingen en de formule van Cardano

Echter ik snap de overgang naar de complexe getallen niet bij het voorbeeld. En heb je die complexe getallen perse nodig om de formule te berekenen?

mich
15-2-2004

Antwoord

Hallo Mich,

De grafiek van een derdegraadsfunctie heeft minimaal 1 en maximaal 3 punten die op de x-as liggen.
Het voorbeeld in het document van P.H. Stikker gaat er van uit dat je de x-coordinaten van deze punten kunt vinden met de methode van Cardano.In dat geval zul je moeten werken met complexe getallen.Je kunt echter ook een oplossing met de formule van Cardano berekenen en dan de factorstelling gebruiken voor de twee andere oplossingen.De factorstelling houdt in dat als x = a een oplossing is dan is de vergelijking deelbaar door (x-a).De uitkomst van deze deling is een tweedegraadsvergelijking.
Hiervoor kun je als het nodig is de abc-formule gebruiken.

Formule van Cardano



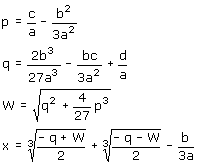
voorbeeld
De vergelijking x³+3x²-9x-27=0 geeft na invullen:
p = -12 ; q = -16 ; w = 0 ; x =3


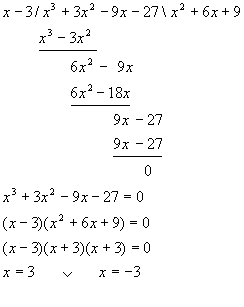
Een alternatief voor de staartdeling is het schema van Horner.

Als q² + 4/27p³ negatief is dan krijgen we alsnog te maken met complexe getallen.

Door de GRM via mode in te stellen op a + bi kunnen we zonder foutmeldingen x berekenen.

wl
16-2-2004