WisFaq!

Lineaire transformatie

Toon aan:
de matrix van de lineaire transformatie Sl, die elk punt van R² spiegelt t.o.v. de rechte LÛ y=mx


is 1/1+m²[1-m²,2m;2m,m²-1]

De tekening die erbij staat ziet er als volgt uit:

op de x-y-stelsel is een hoek getekend. De hoek 'begint' in de oorsprong. de onderzijde van de hoek is de x-as, een hoek a bepaalt de grootte van de hoek met de bovenste zijde van de hoek beschrijft de rechte : LÛ y= mx
In de hoek zelf ligt een punt: a' en boven de bovenste zijde van de hoek gespiegeld: a..


Kan iemand me aub helpen bij deze opgave? Het is niet zo dat ik jullie even mijn huistaak door jullie laat maken maar misschien kan iemand het even mooi uitleggen welke stappen ik moet zetten?

Alvast bedankt,
Anne

Anne
15-2-2004

Antwoord

dag Anne,

De eerste kolom van de matrix is de beeldvector van de vector (1,0).
Je moet dus deze beeldvector berekenen, dat wil zeggen: uitdrukken in m.
Je weet: tan(a) = m
De beeldvector ligt op de lijn y = nx, waarbij de hoek met de positieve x-as dus twee keer zo groot is als a

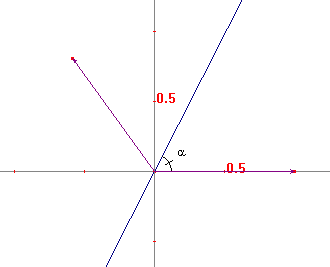
Je weet dus:
n = tan(2a) = 2·tan(a)/(1-tan²(a)) = 2m/(1-m²).
Verder weet je nog dat de beeldvector ligt op een cirkel met middelpunt de oorsprong, en straal 1.
Nu zou het verder moeten lukken.
Succes,

Anneke
16-2-2004