Het probleem waar jij mee te maken hebt is het volgende:
Je combineerde bij een drielandenpunt een drietal spiegelingen. De combinatie van drie spiegelingen in lijnen door een vast punt is weer een spiegeling in een lijn door dat punt. Zo weet je dat het midden van AB zoals je onder 1. beschrijf op zichzelf uit moet komen, en dat de lijn door het hoekpunt en het gevonden midden de spiegellijn is.
Helaas, de combinatie van vier spiegelingen in lijnen door een vast punt is geen spiegeling, maar een rotatie om het vaste punt. Is die rotatie een rotatie over 360 graden, dan is die dat ook voor elk punt in de cel. Daar heb je dan dus niets aan. Sterker nog, als je een voronoi-diagram hebt met alleen vierlandenpunten, dan liggen de "centra" niet eens vast.
Je kunt bijvoorbeeld een Voronoi-diagram met allemaal vierkante cellen samenstellen uit blokken die op de volgende manieren zijn gevuld:
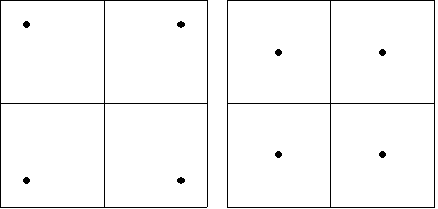
Combinatie van een even aantal spiegelingen wordt een rotatie, van een oneven aantal spiegelingen wordt weer een spiegeling.
Kortom, je hebt drielandenpunten, of eventueel vijflandenpunten, zeven-, ..., nodig.
FvL
10-2-2004