WisFaq!

Willekeurige driehoeken: vraagstuk

twee schepen verlaten gelijktijdig de haven, ieder in een andere richting. Het ene vaart tegen een snelheid van 20 knopen, het andere tegen 17 knopen (1knoop = 1 zeemijl/uur en 1 zeemijl=1852m). na twee uur zijn deze schepen 15 zeemijl van elkaar verwijderd. Bereken de hoek (op 1° afgerond) tussen de vaarrichtingen van beide schepen.

Hannelore Farley
8-2-2004

Antwoord

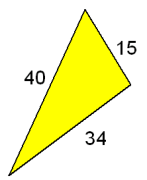
De hoek kan je berekenen met de cosinusregel. In het algemeen geldt voor een driehoek ABC:

a²=b²+c²-2bc·cosa
b²=a²+c²-2ac·cosb
c²=a²+b²-2ab·cosg

In dit geval:



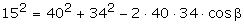
..ff uitrekenen dus...

Zie ook Wat is de sinusregel en de cosinusregel? En hoe bewijs je ze?

WvR
8-2-2004