WisFaq!

Kansen, Venn-diagrammen en kanstabellen

Ik heb twee vragen ter voorbereiding van mijn toetsen maandag.
Ik zou je heel dankbaar zijn als het voor het weekend lukt.

1. In een uitkomsten verzameling met 7 elementen geldt:
   In verzameling A liggen de elementen E1,E2,E3, met elk een kans van 1/5, E5 (kans 1/20) en E6 (kans 1/10).
   In verzameling B de elementen E2,E3 (beide: zie kansen hierboven), E4 (kans (1/20) en E7(kans 1/5)
   
   -Maak een Venn-diagram.
   Bereken de volgende kansen:
   a. P(A) b. P(B) c. P(A of B) d. P(A en B) e. P(niet-A) f. P(niet-B) g. P(A of niet-A) h. P( niet-A en B)

2. 55% van alle Nederlanders eet wel eens patat(P), 40% eet wel eens een frikadel (F), en 35% eet nooit patat en nooit een frikadel.
   
   - Bereken de kans dat iemand patat eet of een Frikadel.Maak een Venn-diagram, noteer het op de juiste manier. (Let op: of betekent: en/of)
   - Bereken de kans dat iemand zowel patat eet als ook frikadel eet.Maak een Venn-diagram, gebruik de additieve regel en noteer het op de juiste manier.
   - Sluiten de gebeurtenissen Patat eten P en Frikadel eten F elkaar uit? Hoe weet je dat?
   Alvast bedankt

nanda
8-3-2002

Antwoord

Venndiagrammen? Nou ik weet niet.. als ik dit soort problemen zie dan maak ik altijd eerst even een kanstabel:



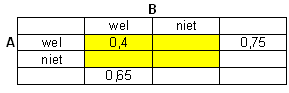
Meteen maar even er in gezet wat ik weet.. en dan kan je de tabel zo invullen.



Daarmee kan je alle vragen zo beantwoorden!
P(niet-B)=0,35
P(A of niet-A)=1
P(niet-A en B)=0,25

Bij die andere vraag kan je ook zo'n tabel maken. Het ziet er dan zo uit:



Eventjes invullen en voila! wederom een opgave opgelost:



P(patat EN frikandel)=0,3

Is zo'n tabel nu iets anders als een Venn-diagram? Nou niet echt. Ik had bij de laatste opgave ook dit Venn-diagram kunnen tekenen:



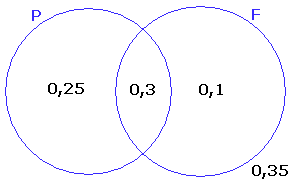
Maar eerst even zo'n tabel is misschien toch wel handig. Ik hoop dat je er iets aan hebt...

WvR
9-3-2002