WisFaq!

Lastig probleem

Ik vroeg (en vraag) mij af of de eigenschap van 2 en 4 dat 2⁴=4² ook geldt voor andere getallenparen. Ik heb al gevonden dat het niet lukt als een van de getallen 1 of 0 is. Daarna heb ik eens geprobeerd om het eens geprobeerd voor 3 maar ik heb geen idee hoe ik de vergelijking zou moeten oplossen.

Mijn vraag is dus, heeft de vgl. 3^x=x³ een oplossing? Zo, ja hoe los je de vergelijking op?

Gertjan Verhaeren
17-1-2004

Antwoord

Exact kan je zo een vergelijking niet oplossen. Daarmee bedoelen we dat je de oplossing niet kan uitdrukken in functies die we als gekend beschouwen, zoals bijvoorbeeld de wortelfunctie. Dat gezegd zijnde, laten we even onderzoeken of er oplossingen bestaan, zonder ze heel exact te kunnen bepalen.

Hiervoor heb je wel een truukje nodig, logaritmen. Die heb je misschien nog niet gezien, maar dan kom je een van de volgende jaren het antwoord maar even herlezen ;)

We zijn op zoek naar twee verschillende positieve reele getallen x en y waarvoor

x^y = y^x
ln(x^y) = ln(y^x)
y·ln(x) = x·ln(y)
ln(x)/x = ln(y)/y

Kan de functie f(t)=ln(t)/t dezelfde waarde aannemen in twee verschillende punten, zijnde t=x en t=y? Daarvoor hebben we de grafiek van f(t) nodig, en die ziet er zo uit.



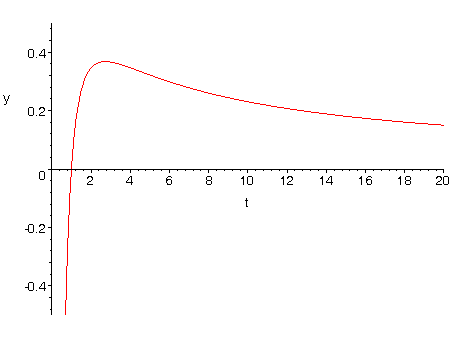
f(t)0 voor t1 en de limiet van f(t) voor t®+¥ is 0. Dat maakt dat voor t1 er geen andere t waarde is die dezelfde functiewaarde oplevert. f(t) heeft verder een maximum voor t=e2,718.

Met elke getal x in het interval ]1,e[ correspondeert dus een ander getal y in het interval ]e,+¥[ dat dezelfde ln(t)/t-waarde heeft. Die getallen x en y voldoen dan aan x^y=y^x.

Als je enkel op zoek bent naar gehele oplossingen, dan volgt uit het feit dat x in ]1,e[ ligt dat x=2 en y=4 de enige mogelijkheden zijn.

cl
17-1-2004