WisFaq!

Fibonacci en de Gulden Snede

Ik ben druk bezig met een praktische opdracht over de Gulden Snede en kan er niet achter komen wat Fibonacci nou met de Gulden Snede te maken heeft. Kunt u mij misschien helpen?

kevin
6-3-2002

Antwoord

Als je kijkt naar de verhouding van opeenvolgende termen van de rij van Fibonacci krijg je een zgn. quotiëntrij. De getallen in deze rij naderen tot een limiet die gelijk is aan .



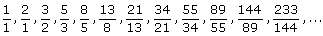
Dit is uitsluitend een gevolg van de regel dat elke term de som van de twee voorafgaande is. Begin met 2 willekeurige termen, contrueer een gegeneraliseerde Finonaccirij en de verhouding van opeenvolgende termen nadert naar .
Woordenboek van eigenaardige en merkwaardige getallen, David Wells

Van de andere kant geldt ook:

Machten van kunnen uitgedrukt worden in :

, ², ³, ⁴,... is hetzelfde als:
, +1, 2+1, 3+2, 5+3, 8+5
Er geldt: ⁿ=^n-1+^n-2. Net als bij de rij van Fibonacci geldt dat een macht van is gelijk aan de som van de 2 voorafgaande termen.

Zie Fibonacci Numbers and the Golden Section [http://www.maths.surrey.ac.uk/hosted-sites/R.Knott/Fibonacci/fib.html]

WvR
6-3-2002