WisFaq!

Integreren met sinus en cosinus

Gegeven is de functie f(x)= 1+2sin(x-1/3$\pi$) en domein [0,2$\pi$]

Bereken de oppervlakte van het vlakdeel dat wordt ingesloten door de grafiek van f en de x-as.

Hiertoe moet je eerst de nulpunten berekenen. dit zou moeten gebeuren met die exacte waardencirkel. tenminste dat denk ik. Met die nulpunten kun je dat heel gemakkelijk de opp bepalen. Ik weet hoe het werkt maar ik kom er niet uit. Ik heb ten lange leste maar met deGR de nulpunten bepaald. Dit bleek1/6$\pi$ te zijn. maar als ik dat vervolgens in mijn geprimitiveerde functie stop komt het niet uit. in het Antw boek staan het volgende antw.: 1 1/3$\pi$ + 2√3 . Ik zelf kom over het algemen op een decimaal getal uit. is dat erg?
groetjes

Mannold
12-1-2004

Antwoord

Eerst oplossen:
1+2·sin(x-¹/₃$\pi$)=0
2·sin(x-¹/₃$\pi$)=-1
sin(x-¹/₃$\pi$)=-¹/₂
x-¹/₃$\pi$=1¹/₆$\pi$ of x-¹/₃$\pi$=1⁵/₆$\pi$
x=1¹/₂$\pi$ of x=¹/₆$\pi$
(denk aan het domein!)

De grenzen zijn ¹/₆$\pi$ en x=1¹/₂$\pi$.



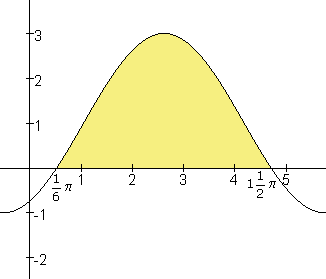
Dus zou je dit moeten uitrekenen:



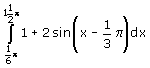
..en volgens mij kan je dat exact. Als dat de vraag is: bereken exact of bereken algebraisch dan moet je dat ook doen. In boeken is deze 'regel' nog niet doorgevoerd, dus in dit geval zou ik proberen het exact uit te rekenen.
Probeer het!

WvR
13-1-2004