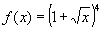
Kunnen jullie deze som aan mij uitleggen en misschien mij in het algemeen uitleggen hoe ik uit een functie het domein en bereik kan halen, alvast bedankt.
Imp
20-7-2001
Mijn vraag is of jullie het volgende aan mij kunnen uitleggen. De som is: Geef de schakels van de kettingfunctie en bepaal daarmee het domein en bereik van de functies.
Kunnen jullie deze som aan mij uitleggen en misschien mij in het algemeen uitleggen hoe ik uit een functie het domein en bereik kan halen, alvast bedankt.
Imp
20-7-2001
domein: de wortel uit een negatief getal kan niet dus x >= 0
bereik: 0 de kleinste waarde is krijg je als ondergrens
en omdat er geen bovengrens is, is het bereik y >= 1
of
domein [0,>
bereik [1,>
In het algemeen is het bereik niet zo eenvoudig te vinden... maar hier wel omdat 'tot de vierde macht' een stijgende functie is op het domein. Als het moelijker wordt kun je een grafiek tekenen of maxima en minima bepalen enz.
Domein en bereik
De verzameling van alle originelen heet domein en de verzameling van beeldenheet bereik.
- Hoe vind je het domein?
- Meestal wordt het domein gegeven. Is dat niet het geval dan kunnen erproblemen ontstaan in enkele van de volgende gevallen:
- In het functievoorschrift komt een wortel voor.
- Het getal onder het wortelteken moet groter of gelijk zijn aan nul.
- Er komt een deling voor in het functievoorschrift.
- Je kunt niet delen door nul. Zorg er voor dat het getal waardoor je deelt niet nul kan worden.
- (wordt vervolgd)
- Hoe vind je het bereik?
- Kijk naar de mogelijke waarden die de functie aan kan nemen op het domein. Hiervoor teken je meestal de grafiek. Eventueel kun je maxima en minima uit rekenen.
Intervalnotatie
Voorbeelden:
[-3,4] alle getallen van -3 tot en met 4 <-3,4] alle getallen tussen -3 en 4 of 4 zelf. <-5, >
alle getallen groter dan -5 [-5, >
alle getallen groter of gelijk aan -5 <¬,Ö2] alle getallen kleiner of gelijk aan Ö2 Voorbeeld domein en bereik
Opdracht Oplossing Grafiek Gegeven is de functie:
Met Df = [-1,3>De grafiek is een parabool.
f(-1) = 2
f(3) = 6
Symmetrie-as: x = ½
Minimum is f(½) = -¼Bepaal het bereik Het bereik is [-¼,6> Wat kan y zijn ?
WvR
20-7-2001
#187 - Functies en grafieken - Leerling bovenbouw havo-vwo