Eerst (Dx)2 buiten haakjes brengen:
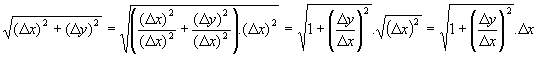
Voor de lengte van de grafiek van de functie f geldt de volgende formule:
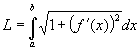
Deze formule staat ook op de formulekaart.
wl
8-1-2004
hoi. Ik zit met het volgende probleem.
Het is de bedoeling dat ik de booglengte ga berekenen. Ik had daar zelf de volgende formule voor gevonden:
åÖ(Dx)2 + (Dy)2. vervolgen kun je er, omdat f'(x) = Dy / Dx , åÖ(Dx)2 + (f'(x))·(Dx)2 van maken. Toch??
Maar nu staat er in mijn boek het volgende:
als je Ö(Dx)2 + (Dy)2 herleid krijg je: Ö1+(f'(x))2 · Dx ( die laatste Dx staat niet meer onder de wortel!!
nu is mijn vraag: waar komt die 1 vandaan. en is mijn herleide functie goed?
alvast bedankt Mannoldmannold
8-1-2004
Hallo Mannold,
Eerst (Dx)2 buiten haakjes brengen:
Voor de lengte van de grafiek van de functie f geldt de volgende formule:
Deze formule staat ook op de formulekaart.
wl
8-1-2004
#18534 - Integreren - Leerling bovenbouw havo-vwo