WisFaq!

Rechthoekige gelijkbenige driehoek in Cabri

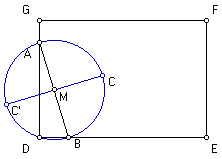
In Cabri moet ik een rechthoekige gelijkbenige driehoek ABC tekenen maar met een extra probleem:

Je begint met een rechthoek DEFG, punt A van de driehoek ligt op DG en punt B van de driehoek ligt op DE. Hoek C ligt in de rechthoek en is 90°.

Zover heb ik het getekend, de bedoeling is echter dat je punt B verplaatsen kan en de zijden van de driehoek even groot blijven. Punt A en B moeten hierbij op repectievelijk DG en DE blijven. Wat je moet bepalen is de baan die het punt C maakt als je punt B over zijde DE verplaatst.

Wat mij nu niet lukt is dat de zijden van de driehoek even groot blijven bij verplaatsing van punt B over DE (de hoeken gelijk houden lukt wel)

Ik hoop dat U mij kan helpen.

met vriendelijke groet.

Kevin Dullemond
15-12-2003

Antwoord

Beste Kevin,

Je kunt gebruik maken van de omgekeerde van de Stelling van Thales. Je krijgt daarmee een goed verplaatsbare constructie, zoals in onderstaande figuur.

Let op, er zijn dus eigenlijk steeds twee plaatsen voor C mogelijk in de figuur. Waarom ligt er altijd maar eentje binnen de rechthoek??

FvL
15-12-2003