Toets of er verschil bestaat tussen versie 1 en 2
versie 1: 10.000 stuks verstuurd, responsepercentage 0,15%, versie 2: 12.000 stuks verstuurd, responsepercentage 0,20%,
We berekenen eerst de gezamelijke fractie:
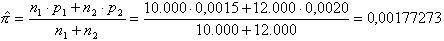
Deze fractie gebruik je vervolgens om de maximale grens voor het verschil in de fracties in de steekproef vast te stellen.
Deze grens bedraagt bij 95% betrouwbaarheid (z=1,96)
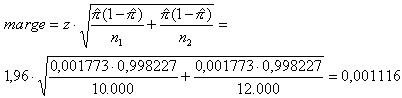
Dat betekent dat een verschil tot 0,001116 in de twee waargenomen fracties aan het toeval kan liggen.
Je wil nu toetsen of de werkelijke fracties significant verschillen. Nulhypothese is dat deze fracties in werkelijkheid niet verschillen. Het verschil tussen de fracties in de steekproef bedraagt: 0,0020-0,0015=0,0005. Aangezien deze waarde kleiner is dan de toevalsmarge (0,001116) betekent dit dat er geen significant verschil aangetoond kan worden.
Wellicht kun je hier alleen aantonen dat het verschil tussen 1 en 3 significant is.
Een toets die meer dan twee fracties tegelijk toetst is mij niet bekend.
Natuurlijk zou je dit vrij eenvoudig met excel kunnen maken.
Deze toets heet in het engels: Test for differences between proportions. In de uitvoering zijn varianten mogelijk (die feitelijk op hetzelfde neerkomen). De toets zit niet in SPSS, wel kun je in plaats van deze toets met SPSS een chi-kwadraattoets op onafhankelijkheid in een kruistabel uitvoeren. De oplossing via excel lijkt me in jouw geval een betere.
Met vriendelijke groet
JaDeX
jadex
14-12-2003