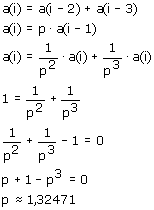
Dit geeft dan de reeks:
10; 13,25; 17,55; 23,25; ...
..en die blokkendoos dat... eh.. weet ik niet...

WvR
25-2-2002
Met het volgende vraagstuk uit mijn PO had ik moeite:
H. van der Laan had kritiek op de modulor. Hij vond dat de modulor alleen voor een verdeling van 2-dimensionale vlakken geschikt was. Van der Laan ontwierp een 3D-maatstelsel, dat de wetmatigheden a(i)=a(i-2)+a(i-3) en a(i)=p·a(i-1) bevat. Dit leidt voor p tot 'het plastisch getal', vergelijkbaar met de gulden snede.
Leid uit de twee gegeven wetmatigheden af dat het plastisch getal ongeveer 1.325 is.
Stel je voor dat de kleinste maat in het stelsel 10 cm is. Tot welke maten leidt een dergelijk stelsel?
Deze maten zijn maten voor blokken. Kun je een blokkendoos, waarmee de architect kan spelen, ontwerpen?Emmy Hertogh
24-2-2002
Herhaald toepassen van a(i)=p·a(i-1) levert:
Dit geeft dan de reeks:
10; 13,25; 17,55; 23,25; ...
..en die blokkendoos dat... eh.. weet ik niet...
WvR
25-2-2002
#1677 - Fibonacci en gulden snede - Leerling bovenbouw havo-vwo