WisFaq!

3x3 stelsels

We hebben deze oefening in de klas ook gemaakt maar dan met substitutie nadien, maar mijn leerkracht zei ook dat je dat met matrixen verder kon uitwerken, wat we vorig schooljaar gezien hebben, het probleem is dat ik niet verder kan.

x+3y-2z=13
3x-y+z=-2
2x+2y-3z=15

1  3  -2  13
3  -1  1  -2
2  2  -3  15

R2-3R1
®
R3-2R1

1    3  -2   13
0  -10   7  -41
0   -4   1  -11

4R2
®
10R3

1   3    -2    13
0  -40  +28  -164
0  -40   10  -110

R3-R2
®

1    3   -2    13
0  -40   28  -164
0    0  -18    54

tot hier en dan hebben we het met substitutie gemaakt aar ik wil hier verder gaan in matrixen
wat ik al heb:

R3:(-18)
®

1    3  -2    13
0  -40  28  -164
0    0   1    -3

R2:(-4)
®

1   3  -2  13
0  10  -7  41
0   0   1  -3

R2-3R1

1   3  -2  13
-3  1  -1   2
0   0   1  -3

...? dank u

Steven De Saedeleer
22-11-2003

Antwoord

Als je het stelsel vergelijkingen in matrix-vorm omzet en daarmee verder rekent door de matrix “schoon te vegen”, dan blijven gewoon dezelfde regels gelden als bij het stelsel vergelijkingen.

Je mag dus:
- de hele rij met een constante vermenigvuldigen of door een constante delen
- rijen van elkaar aftrekken of bij elkaar optellen
- rijen verwisselen

De algemene aanpak is vaak dat je zorgt dat in de linker onderhoek allemaal nullen komen te staan.
Aan het eind wil je dan een matrix met op de diagonaal 1-en en voor de rest 0-en

Je bent al een heel eind gekomen:

x+3y-2z=13
3x-y+z=-2
2x+2y-3z=15

Dit kunnen we schrijven als:

*

=

We gaan in verkorte notatie verder:



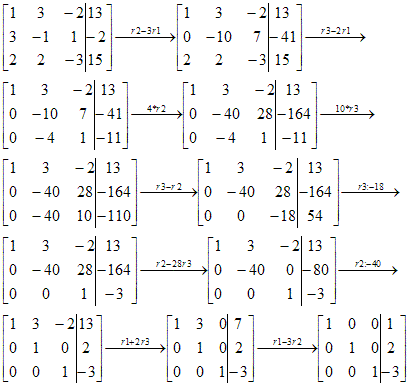
Zoals je ziet was je er echt bijna.

Wil je nog een voorbeeld uitgewerkt zien, kijk dan bij onderstaande link.
Stelsel vergelijkingen oplossen met matrix-notatie

gm
23-11-2003