WisFaq!

Vraagstuk over twee ladders in een steeg

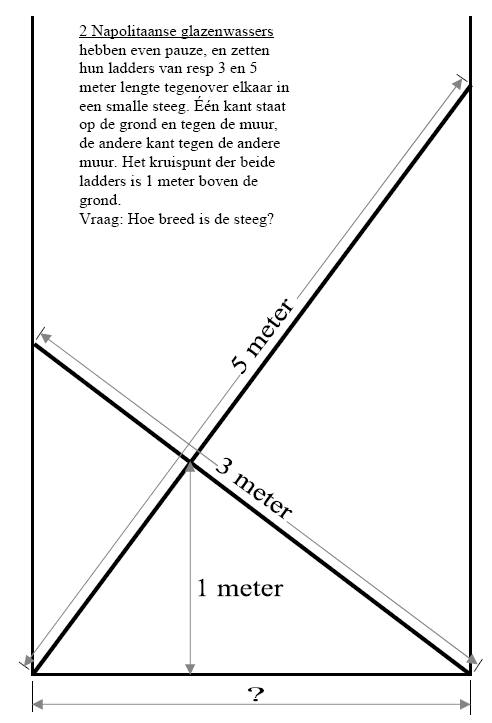
Het vraagstuk van de twee ladders, staand in een steeg. De ladderlengtes zijn bekend, evenals de hoogte van het kruispunt van de twee ladders. De steegbreedte is hier de vraag.



Rekenen daaraan ontaardt in een eindeloze reeks vergelijkingen, zonder enig zicht op een bevredigende oplossing. Waarom is dat?

Theo Lutgerink
10-11-2003

Antwoord

Het ligt er maar net aan wat je bevredigend noemt.
Je kunt het probleem vertalen in een stelsel vergelijkingen.
Het is nu eenmaal zo, dat er vergelijkingen zijn die er best simpel uitzien, maar die behoorlijk ingewikkeld zijn op te lossen.

Galois heeft daar een hele theorie op gebouwd.
Eerst maar even een pragmatische aanpak.
In dit geval zou je de volgende twee vergelijkingen kunnen opstellen:

Noem het gedeelte van de breedte van de steeg vanaf de linkermuur tot het ladderkruispunt: a, en de rest van de steeg: b.

Dan gelden de volgende vergelijkingen:

a + b = 9·b²/√(b²+1)
a + b = 25·a²/√(a²+1)

Dit stelsel levert als benaderde oplossing:

a $\approx$ 0.6409506791
b $\approx$ 2.057156238

wat leidt tot het antwoord: de breedte van de steeg is:
a+b $\approx$ 2.698106917 meter.

Op onderstaande site vind je een uitgebreid antwoord op je vraag.

• Een steeg en twee ladders

groet

Anneke
10-11-2003